Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 13
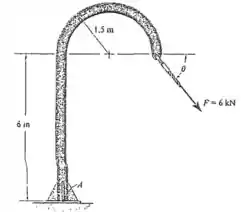
Determine o momento produzido pela força em relação ao ponto em função do ângulo . Construa o gráfico de em função de , onde.
Passo 1
Para determinar o momento gerado pela força é necessário determinar a distância do ponto até o ponto de atuação da força onde os momentos serão aplicados. Assim, os eixos e serão considerados respectivamente a linha horizontal e a linha vertical.
Logo, para a componente horizontal da força, a distância até o braço do momento será de:
E para a componente vertical da força será de:
Passo 2
Dessa forma, dividindo a força em suas componentes horizontal e vertical e aplicando o princípio dos momentos considerando que os momentos positivos agem no sentido anti-horário, tem-se que:
no sentido horario
Passo 3
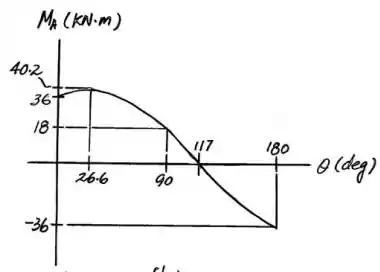
Agora, pode-se adotar alguns pontos a serem definidos e plotados no gráfico que se deseja construir. Tais pontos podem ser os valores nulo e máximo do momento e os valores , e .
Passo 4
Dessa forma, o momento máximo ocorrerá quando , tal que:
Rearranjando esta equação:
Portanto,
E quando o momento for nulo:
Passo 5
E para cada valor de pré definido, tem-se que:
Logo, com todas essas informações definidas é possível desenhar o gráfico do momento em função do ângulo .
Resposta
no sentido horário
