Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 12

3.12. A porta traseira de um carro é sustentada por uma haste hidráulica BC. Se a haste exerce uma força de 566   N dirigida ao longo de sua linha de centro sobre a rótula em B, determine o momento da força em relação a A.

Passo 1

Bem, quase todo exercício de mecânica fica mais simples resolver se fizermos um desenho da situação destacando o que a gente precisa.

A gente tem uma força ao longo de C B e para decompor essa força precisamos trabalhar com seno e cosseno. Vamos pegar o triângulo

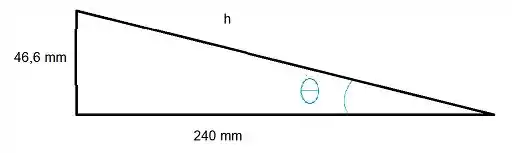
Se a gente conseguir determinar a hipotenusa, a gente consegue achar os valores de seno e cosseno desse ângulo. Para isso vamos precisar de uma ajudinha de Pitágoras. Mas antes vamos colocar tudo em metros

46,6   m m = 0,0466   m

240   m m = 0,24   m

Então

h = 0,0466 2 + 0,24 2 = 0,244   m

Logo

cos ⁡ θ = 0,24 0,244

E

sin ⁡ θ = 0,0466 0,244

Então a gente tem

F C B = F C B cos ⁡ θ   î - F C B sin ⁡ θ   j ^

F C B = 556   0,24 0,244   î - 556   0,0466 0,244   j ^

F C B = 546,88   î - 106,18   j ^ N

Passo 2

O momento de uma força é definido por

M = d × F

Onde

M = Momento

F =   Força

d = distância

Bem essa distância é do ponto onde a força está sendo aplicado até o ponto onde queremos medir o momento, em outras palavras, é o vetor r B A →

r B A → = 0,306 î - 0,24 + 0,0466   j ^   m

r B A → = 0,306 î - 0,2866   j ^   m

Agora a gente pode fazer esse produto vetorial tranquilo

î j ^ k ^ 0,306 - 0,2866 0 546,88 - 106,18 0

Por Laplace

M = 0   î + 0   j ^ + - 0,306 ⋅ 106,18 + 0,2866 ⋅ 546,88   k ^

M = 124,244   N ⋅ m

No sentido anti-horário.

Resposta

M = 124,244   N ⋅ m

No sentido anti-horário.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As pinças são usadas para prender as extremidades do tubo de perfuração P . Determine o torque (momento) M P que a força apliada F = 750N exerce sobre o tubo em relação ao ponto P como uma função de θ
Sérios danos ao pescoço podem ocorrer quando um jogador de futebol americano é atingido na proteção de rosto de seu capacete da maneira mostrada, causando um mecanismo de guilhotina. Determine o momen
Determine o momento da força F em relação ao ponto A como uma função de θ . Represente os resultados de M (ordenada) em função de θ (abscissa) para ( 0 ° ≤ θ ≤ 180 ° ) .
Determine o ângulo θ ( 0 ° ≤ θ ≤ 180 ° ) da força F de modo que ela produza um momento máximo e um momento mínimo em relação ao ponto A . Além disso, quais são as intensidades desses momentos máximo e
Determine o momento produzido pela força F em relação ao ponto A em função do ângulo θ . Construa o gráfico de M A em função de θ , onde ( 0 ° ≤ θ ≤ 180 ° ) .