Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 21
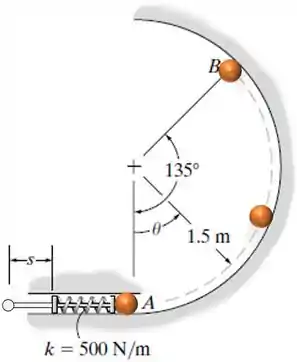
A bola de 0,5 kg de dimensão desprezível é lançada para cima na pista circular vertical lisa usando o pistão com mola. O pistão mantém a mola comprimida 0,08 m quando . Determine até que ele deve ser puxado para trás e solto de maneira que a bola vá começar a deixar a pista quando .
Passo 1
O enunciado nos deu as seguintes informações:
Massa da bola: kg;
Pista lisa: força de atrito desprezível.
Para , a mola esta comprimida m.
Devemos determinar o valor de para o qual a bola irá deixar a pista em , ou seja, quando a força normal seja nula () neste ponto.
Primeiramente, vamos desenhar o diagrama de corpo livre da bola no instante em que :
Onde é a força peso e é a força normal. Como é um movimento circular, teremos a ação da aceleração normal .
Passo 2
Vamos aplicar a Equação de Movimento:
Em :
Sabemos que
Logo, podemos descrobrir a velocidade da bola no ponto .
Passo 3
Agora vamos aplicar o Princípio do Trabalho e Energia para descobrir o valor de .
Assumimos que, inicialmente, a bola estava em repousou, portanto .
O trabalho exercido pela mola é positivo, uma vez que empurra a bola no mesmo sentido do deslocamento. A força é dada como . Para ,
A força peso, por outro lado, exercerá um trabalho negativo, pois age sobre a bola no sentido oposto ao deslocamento dela. No ponto onde ,
Temos que
onde
Substituindo esses valores na equação inicial, obtemos
A raíz positiva da equação de segundo grau acima nos da o seguinte valor: