Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 26
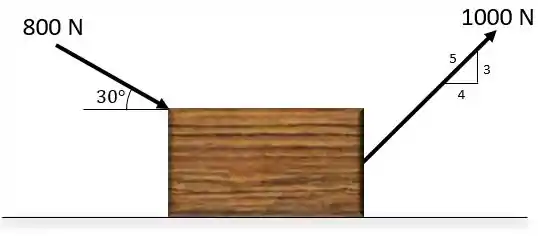
A caixa, que tem massa de 100 kg, é submetida à ação das duas forças. Se ele está originalmente em repouso, determine a distância que ele desliza a fim de alcançar uma velocidade de 6 m/s. O coeficiente de atrito cinético entre a caixa e a superfície é .
Passo 1
O enunciado nos dá as seguintes informações:
Massa da caixa: kg;
Originalmente em repouso: ;
Velocidade final: ;
Coeficiente de atrito:
Devemos determinar a distância que a caixa deliza até alcançar a velocidade .
Iniciamos a questão desenhando o diagrama de corpo livre da caixa:
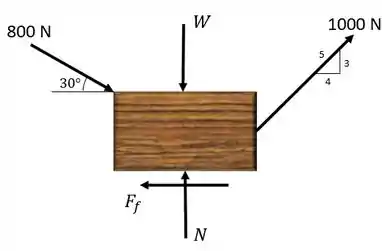
Onde é a força peso, é a força normal e é a força de atrito.
Passo 2
Primeiramente, vamos aplicar as equações de movimento:
No eixo :
Passo 3
Agora iremos utilizar o Princípio do Trabalho e Energia:
A caixa se desloca horizontalmente, portanto todas as forças que possuem componentes nesta direção, realizarão trabalho sobre ela. Logo, a força peso, a força normal e as componentes verticais das forças de 800 N e 1000 N não exercerão trabalho sobre a caixa.
A forças de atrito terá sentido oposto ao deslocamento da caixa, logo o trabalho realizado por ela será negativo.
Temos que
onde
Substituindo esses valores na equação inicial, obtemos