Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 24
O bloco de 1 kg desliza para baixo pela superfície parabólica lisa de tal maneira que quando ele está em ele tem uma velocidade de 3 m/s. Determine a intensidade da velocidade e aceleração do bloco quando ele chega ao ponto , e a altura máxima alcançada pelo bloco.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do bloco: 1 kg;
Superfície lisa: força de atrito desprezível;
Velocidade em : m/s;
Trajetória: .
Devemos determinar a intensidade da velocidade e aceleração do bloco quando ele chega ao ponto e a altura máxima atingida por ele em .
Incialmente, desenhamos o diagrama de corpo livre do bloco nos pontos e , respectivamente:
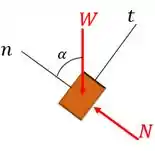
Onde é a força peso e é a força normal.
Como a trajetória é circular, o corpo sofrerá uma aceleração normal .
Passo 2
Primeiramente, vamos analisar os dados no Ponto
Sabemos que , logo
Aplicando o Princípio do Trabalho e Energia, temos
onde
Substituindo esses valores na equação inicial, obtemos
Passo 3
Agora, precisamos encontrar a aceleração do bloco em .
Esta aceleração é composta por uma componente tangencial e uma normal:
Nesta parte da resolução, utilizaremos as Equações de Movimento, porém, precisamos descobrir o ângula primeiro.
Sabemos que
Para , , resultando em
No eixo , temos:
Sabemos que
E que
Logo, no ponto ,
Portanto, .
Passo 4
Agora, precisamos encontrar a altura máxima atingida pelo bloco em .
Como neste ponto o bloco atinge altura máxima, sua velocidade será nula ().
Aplicando o Princípio do Trabalho e Energia, temos
onde
Substituindo esses valores na equação inicial, obtemos