Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 29
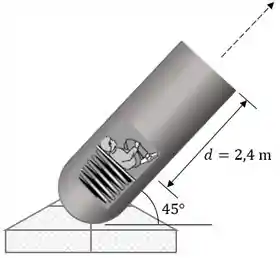
O homem de 60 kg atua como uma bala de canhao humana ao ser ‘atirado’ do canhão armado com uma mola como mostrado. Se a maior aceleração que ele pode sentir é , determine a rigidez necessária da mola que está comprimida 0,6 m no momento do lançamento. Com que velocidade ele vai deixar o cano do canhão, m, quando o canhão for disparado? Quando a mola é comprimida de m, então m. Despreze o atrito e suponha que o homem se mantém em uma posição rígida durante todo o movimento.
Passo 1
O enunciado nos dá as seguinte informações:
Massa do homem: kg;
Aceleração máxima sobre o homem: ;
Mola comprimida: m;
Devemos determinar a velocidade com que o homem irá deixar o canhão quando ele for disparado. Neste momento, m.
Inicialmente, vamos desenhar o diagrama de corpo livre do homem no dentro do canhão:
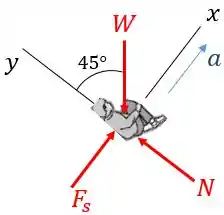
Onde é a força peso, é a força normal e é a força elástica exercida pela mola.
Passo 2
Primeiramente, vamos descobrir o valor da força da mola, pois sabemos que esta força irá exercer trabalho sobre o homem.
Para isso, vamos utilizar as Equações do Movimento:
No eixo :
Sabemos que , logo
Passo 3
Agora que já temos as informações sobre as forças e sobre a mola, vamos aplicar o Princípio do Trabalho e da Energia para encontrar a velocidade do homem ao sair do canhão.
No primeiro momento, o homem está em repouso, logo sua velocidade inicial é nula.
A mola exercerá um trabalho positivo sobre o homem, pois o está empurrando no mesmo sentido do deslocamento. Já a força peso exercerá trabalho negativo, pois atua no sentido oposto.
Temos que
onde
Substituindo esses valores na equação inicial, obtemos