Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 27
O tijolo de 1 kg desliza para baixo por um telhado liso de tal maneira que quando ele está em tem velocidade de 1,5 m/s. Determine a velocidade do tijolo imediatamente antes de ele deixar a superfície em , a distância da parede até ele atingir o solo e a velocidade com a qual ele bate no solo.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do tijolo: kg;
Telhado liso: força de atrito desprezível;
Velocidade em : m/s.
Devemos determinar:
a velocidade do tijolo imediatamente antes de ele deixar a superfície em ;
a distância da parede até ele atingir o solo;
a velocidade com a qual ele bate no solo.
Inicialmente, desenharemos o diagrama de corpo livre do tijolo no trecho :
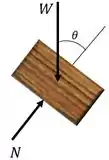
Onde é a força peso e é a força normal exercida pelo telhado sobre o tijolo.
Passo 2
Vamos começar nossa análise pelo trecho .
Primeiramente, vamos aplicar o Princípio do Trabalho e da Energia para descobrir a velocidade do tijolo no ponto .
Temos que
onde
Substituindo esses valores na equação inicial, obtemos
Passo 3
Agora queremos encontrar a distância que o tijolo percorre ao sair de e atingir o solo.
Para isso, podemos utilizar as seguintes equações conhecidas:
No eixo :
No eixo :
A raíz positiva desta equação do segundo grau nos dá o seguinte valor para :
Logo, obtemos
Passo 4
Em seguida, vamos analisar o trecho para encontrar a velocidade do tijolo ao tocar o solo.
Para isso, utilizaremos o Princípio do Trabalho e da Energia.
Temos que
onde
Substituindo esses valores na equação inicial, obtemos