3/136) Um carro de está viajando a uma velocidade quando passa o ponto , e em seguida o carro desce umainclinação de . O motorista aciona os freios de modo a trazer a velocidade do carro em para . Calcule a energia dissipada pelos freios na forma de calor . Despreze as perdas por atrito devido a outras causas como , por exemplo , a resistência do ar .
Passo 1
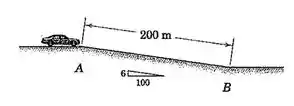
Bom pessoal , a prieira coisa que devemos fazer é achar o ângulo de inclinação da pista indicada na imagem . Para isso , temos que :
Agora devemos lembrar da equação de trabalho-energia , na qual :
Passo 2
Então galera , isolando na equação e substituindo os valores que já conhecemos :
Reparem que o sinal negativo indica que houve perda de energia , nesse caso , de módulo :
Resposta
De boa galera? Bora fazer mais exercícios então!