Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 14
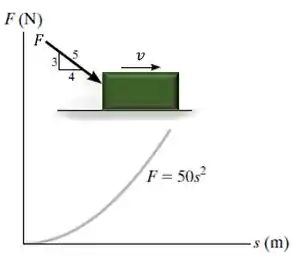
A força , atuando em uma direção constante sobre o bloco de 20 kg, tem uma intensidade que varia com a posição do bloco. Determine a distância que o bloco desliza antes que sua velocidade se torne 5 m/s. Quando , o bloco está se deslocando para a direita à 2 m/s. O coeficiente de atrito cinético entre o bloco e a superfície é .
Passo 1
O enunciado nos dá as seguintes informações:
Massa do bloco: ;
Coeficiente de atrito cinético: .
Além disso, para temos .
Devemos determinar a distância que o bloco desliza antes que sua velocidade chegue à .
Inicialmente, desenhamos o diagrama de corpo livre do bloco:
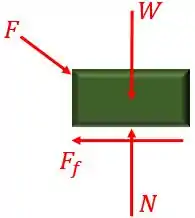
Onde é a força peso, é a força de atrito e é a força normal.
Passo 2
Agora, vamos utilizar a Equação do Movimento.
No eixo :
Passo 3
Aplicando o Princípio de Trabalho e Energia, obtemos
Logo,
Substituindo estes valores na equação principal, temos que
Chegamos a seguinte equação de terceiro grau:
Onde a raiz real nos dá o valor de
Esta é a distância que o bloco deslizou antes de atingir a velocidade de 5 m/s.