Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 14

3.14. Um mecânico utiliza um pedaço de tubo AB como alavanca para esticar a correia de um alternador. Quando ele empurra a alavanca para baixa em A, uma força de 485   N é exercida sobre o alternador em B. Determine o momento dessa força em relação ao parafuso C se a sua linha de ação passa através de O.

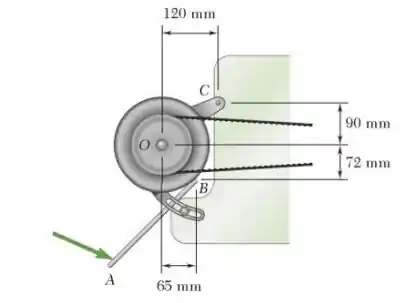
Passo 1

Bem, quase todo exercício de mecânica fica mais simples resolver se fizermos um desenho da situação destacando o que a gente precisa.

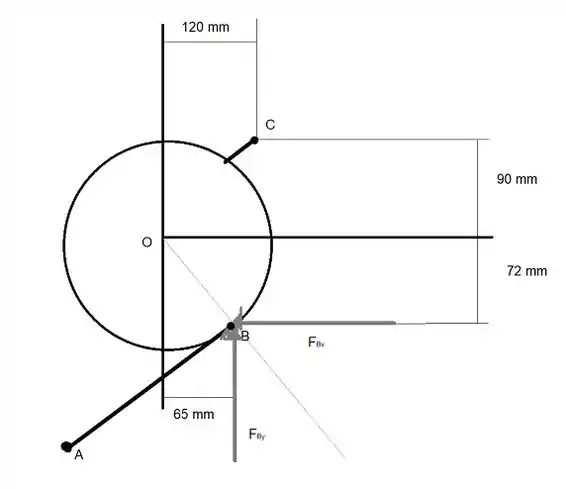
Como a linha de ação da força cruza o ponto O, podemos extrair esse tirângulo para nos ajudar a decompor a força

Vamos determinar a hipotenusa, mas antes vamos passar tudo para metros

72   m m = 0,072   m

65   m m = 0,065   m

h = 0,072 2 + 0,065 2 = 0,097   m

E agora podemos determinar o seno e o cosseno desse ângulo

cos ⁡ θ = 0,065 0,097

sin ⁡ θ = 0,072 0,097

Agora a gente pode decompor a força

F x = F ⋅ cos ⁡ θ

F x = 485 ⋅ 0,065 0,097 = 325   N

F y = 485 ⋅ 0,072 0,097 = 360   N

Passo 2

O momento de uma força é definido por

M = d ⋅ F

Onde

M = Momento

F =   Força

d = distância

Já que decompomos a força vamos fazer

M = M x + M y

Vamos calcular M x

M x = F B x ⋅ y

M x = 325 ⋅ 0,072 + 0,09 = 52,65   N ⋅ m

E agora M y

M y = F B y ⋅ x

M y = 360 ⋅ 0,12 - 0,065 = 19,8   N ⋅ m

Então

M = 52,65 + 19,8 = 72,15   N ⋅ m

Mas repare que todas as forças produzem um efeito de rotação no sentido horário.

Resposta

M = 72,15   N ⋅ m

No sentido horário.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A fim de erguer o poste de iluminação a partir da posição mostrada, a força F é aplicada ao cabo. Se F = 1000N , determine o momento produzido por F em relação ao ponto A .
A região do pé está sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.
A força de 70N age no final do tubo B . Determine ( a ) o momento dessa força em relação ao ponto A e ( b ) a intensidade e a direção de uma força horizontal, aplicada em C , que produz o mesmo moment
A lança do elevador é estendida até a posição mostrada. Se o operário pesa 800N ( ≈ 80k g ) , determine o momento dessa força em relação à conexão em A .
Sabe-se que é necessária uma força com um momento de 960 N ⋅ m em relação a D para endireitar o mourão CD. Se d=2,8 m, determine a tração que deve ser desenvolvida no cabo do guincho A B para criar o