Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 26

A região do pé está sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.

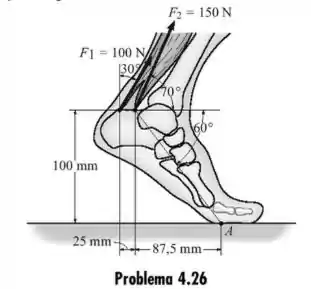
Passo 1

Fala galerinha, tudo certo? Bora começar desenhando o diagrama de corpo livre desse pé!

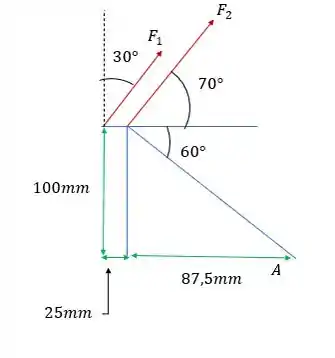
Os momentos gerados pela forças podem ser determinados decompondo as forças perpendiculares as distâncias, então vamos definir as decomposições das forças:

Para F 1 :

F 1 x = F 1 s e n θ 1

F 1 y = F 1 c o s θ 1

E para F 2 :

F 2 x = F 2 c o s θ 2

F 2 y = F 2 s e n θ 2

Detalhe que aqui as identidades trigonométricas ficaram alternadas pois os ângulos se encontram em posições diferentes em relação as forças.

Além disso, vale lembrar que o momento é dado por:

M = F   d

Passo 2

A partir disso, tomando o momento como positivo no sentido horário, o momento gerado pela força F 1 em relação ao ponto de interesse é dado pelos momentos causados pelas suas componentes:

M A 1 = F 1 y 0,1125   m + F 1 x 0,1   m

M A 1 = F 1 cos ⁡ 30 ° 0,1125   m + F 1 s e n 30 ° 0,1   m ( h o r á r i o )

Tal que:

M A 1 = 100 cos ⁡ 30 ° 0,1125   m + 100 s e n 30 ° 0,1   m

⇒ M A 1 = 14,74   N ∙ m ( h o r á r i o )

Da mesma forma, para a força F 2 , o momento gerado é:

M A 2 = F 2 x 0,1   m + F 2 y 0,0875   m

Tal que:

M A 2 = F 2 cos ⁡ 70 ° 0,1   m + F 2 s e n 70 ° ( 0,0875   m )

Ou seja:

M A 2 = 150 cos ⁡ 70 ° 0,1   m + 150 s e n 70 ° ( 0,0875   m )

⇒ M A 2 = 17,46   N ∙ m

Resposta

M A 1 = 14,74   N ∙ m no sentido horário

M A 2 = 17,46   N ∙ m no sentido horário

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A grua torre é usada para içar a carga de 2 Mg para cima em velocidade constante. A lança BD de 1,5 Mg, a lança BC de 0,5 Mg e o contrapeso C de 6 Mg possuem centros de massa em G1, G2 e G3, respectiv
Os relógios antigos eram construídos usando uma polia B em forma de cone para impulsionar as engrenagens e os ponteiros do relógio. A finalidade dessa polia é aumentar a alavanca desenvolvida pela mol
A lança do elevador tem um comprimento de 9  m, uma massa de 400 kg e centro de massa em G. Se  o momento máximo que pode ser desenvolvido por  um motor em A é M = 30 kN.m, determine a carga máxima W,
O poste do exercício anterior é fixado na posição vertical com 15 por cento de seu comprimento dentro da base de concreto e solicitado através de um cabo que exerce uma força F em sua extremidade supe
0 vento exerce uma força uniformemente distribuída de 0,6k N / m 2 na superfície do painelesquematizado na próxima figura. Reduza essa força à base da coluna de suporte desse painel