Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 15

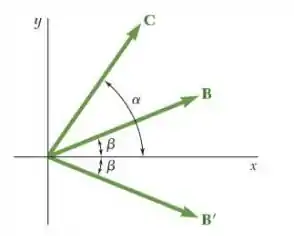
3.15. Desenvolva os produtos vetoriais B × C e B ' × C , onde B = B ' , e use os resultados obtidos para demonstrar a identidade:

sin ⁡ α cos ⁡ β = 1 2 sin ⁡ α + β + 1 2 sin ⁡ α - β

Passo 1

Bom, vamos começar decompondo as forças nos eixos. A gente tem o módulo dos vetores e os ângulos, então a gente consegue

B = B cos ⁡ β   î + sin ⁡ β j ^

B ' = B cos ⁡ β   î - sin ⁡ β j ^

C = C ( cos ⁡ α î + sin ⁡ α   j ^ )  

Agora vamos relembrar algumas propriedades do produto vetorial que serão importantes

B × C = B ⋅ C ⋅ sin ⁡ α - β

B ' × C = B ⋅ C ⋅ sin ⁡ α + β

Passo 2

Beleza, agora a gente pode começar a desenvolver as contas, vamos fazer

B × C = B cos ⁡ β   î + sin ⁡ β j ^ × C ( cos ⁡ α î + sin ⁡ α   j ^ )  

Vamos fazer uma matriz para ajudar a visualizar esse produto vetorial

î j ^ k ^ B cos ⁡ β B sin ⁡ β 0 C cos ⁡ α C sin ⁡ α 0

Esse determinante vai dar

B C cos ⁡ β sin ⁡ α - sin ⁡ β cos ⁡ α k ^

Ou seja

B × C = B C cos ⁡ β sin ⁡ α - sin ⁡ β cos ⁡ α

Mas relembrando que

B × C = B ⋅ C ⋅ sin ⁡ α - β

Então

B C cos ⁡ β sin ⁡ α - sin ⁡ β cos ⁡ α = B C sin ⁡ α - β

Passo 3

Vamos fazer uma coisa muito parecida para B ' × C

B ' × C = B cos ⁡ β   î - sin ⁡ β j ^ × C ( cos ⁡ α î + sin ⁡ α   j ^ )  

Vamos fazer uma matriz para ajudar a visualizar esse produto vetorial

î j ^ k ^ B cos ⁡ β - B sin ⁡ β 0 C cos ⁡ α C sin ⁡ α 0

Esse determinante vai dar

B C cos ⁡ β sin ⁡ α + sin ⁡ β cos ⁡ α k ^

Ou seja

B ' × C = B C cos ⁡ β sin ⁡ α + sin ⁡ β cos ⁡ α

Mas relembrando que

B ' × C = B ⋅ C ⋅ sin ⁡ α + β

Então

B C cos ⁡ β sin ⁡ α + sin ⁡ β cos ⁡ α = B C sin ⁡ α + β

Passo 4

Agora que temos as equações

B C cos ⁡ β sin ⁡ α - sin ⁡ β cos ⁡ α = B C sin ⁡ α - β

B C cos ⁡ β sin ⁡ α + sin ⁡ β cos ⁡ α = B C sin ⁡ α + β

Vamos soma-las

B C cos ⁡ β sin ⁡ α + sin ⁡ β cos ⁡ α + B C cos ⁡ β sin ⁡ α - sin ⁡ β cos ⁡ α

= B C sin ⁡ α + β + B C sin ⁡ α - β

A gente pode cortar B C

cos ⁡ β sin ⁡ α + sin ⁡ β cos ⁡ α + cos ⁡ β sin ⁡ α - sin ⁡ β cos ⁡ α = sin ⁡ α + β + sin ⁡ α - β

Isso vai dar

2 cos ⁡ β sin ⁡ α = sin ⁡ α + β + sin ⁡ α - β

Agora a gente passa o 2 dividindo e

sin ⁡ α = 1 2 α + β + 1 2 sin ⁡ α - β

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

36. O carrinho de mão e seu conteúdo possuem centro de massa em G. Se F = 100N e o momento resultante produzido pela força F e peso em relação ao eixo A é zero, determine a massa do carrinho e de seu
30. Se F B = 150N e F C = 225N , determine o momento resultante em relação ao parafuso localizado em A.
32. O cabo de reboque exerce uma força P = 4k N na extremidade da lança do guindaste de 20 m de comprimento. Se θ = 30 ° , determine o posicionamento x do gancho em A para que essa força crie um momen
28. A força de 70N age na extremidade do tubo em B. Determine os ângulos θ ( 0 ° ≤ θ ≤ 180 ° ) da força que produzirá os momentos máximo e mínimo em relação ao ponto A. Quais são as intensidades desse
A fim de erguer o poste de iluminação a partir da posição mostrada, a força F no cabo deve ciar um momento de 2250N ∙ m no sentido anti-horário em relação ao ponto A . Determine a intensidade de F que