Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 16
3.16. Uma linha passa pelos pontos e . Determine a distância perpendicular d da linha até a origem O do sistema de coordenadas.
Passo 1
Vamos começar fazendo um desenho do que está acontecendo:
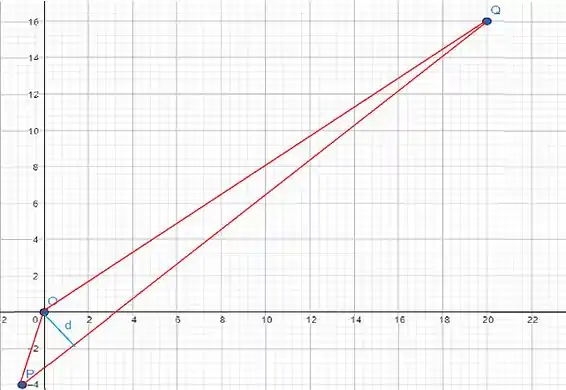
A gente quer determinar essa distância d.
A gente pode imaginar que tem uma força agindo na linha , e calcular o momento que essa força exerce na origem, ai podemos achar a distância. Parece um pouco estranho mas vai dar certo.
Passo 2
Vamos lá, começamos definindo
Sendo que é um versor que aponta na direção . Vamos definir esse versor
Então
E também precisaremos da distância para fazer nosso produto vetorial vamos precisar também de
Passo 3
Agora a gente pode definir o momento da força aplicada em A em relação a origem.
E isso vai ser igual a
Já que é perpendicular à .
Vamos lá
Por Laplace
Como o momento está em uma única direção, esse valor é igual seu módulo, por tanto
Olha que coisa boa, a gente pode cortar o F
Então