Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 12
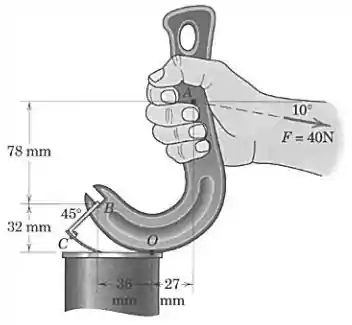
A ferramenta mostrada é projetada para ajudar a remover tampas de latas com argolas. Se o usuário exerce uma força de em , determine a força trativa na parte da argola.
Passo 1
Podemos decompor a força em uma força horizontal para a direita e uma força vertical para baixo, onde ambas produzem momento em torno de no sentido horário (negativo). Então, o momento da força em torno de será:
Passo 2
Analogamente, obtemos a expressão do momento da força em torno de , somando os momentos de suas componentes, que ocorrem no sentido anti-horário (positivo):
Lembre-se sempre de padronizar as unidades. Aqui estamos usando somente newtons e milímetros.
Passo 3
Por fim escrevemos a equação de equilíbrio de momentos, onde a soma de todos os momentos em torno de deve ser nula: