Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 13

Um lenhador deseja fazer o tronco da árvore cair para cima do morro, apesar do tronco estar inclinado para baixo. Com a ajuda do guincho , qual será a força trativa necessária no cabo? O tronco de tem centro de massa em . O corte em é suficientemente profundo, de modo que o momento de reação nesse ponto é desprezível.

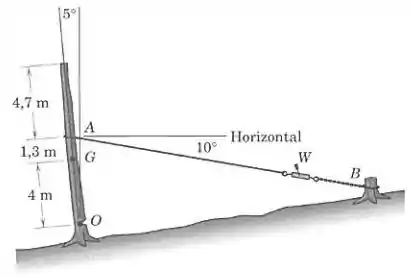
Passo 1

Pela figura, vemos que a força peso atuando em (vertical) faz um ângulo de com a linha do tronco. Então, o momento do peso em relação ao ponto ocorre no sentido anti-horário (positivo) e é dado pela fórmula:

Passo 2

Analogamente, obtemos a expressão do momento da força em torno de , que ocorre no sentido horário (negativo). Pela geometria da figura, a força trativa faz um ângulo de com a linha do tronco:

Lembre-se sempre de padronizar as unidades. Aqui estamos usando somente newtons e metros.

Passo 3

Por fim escrevemos a equação de equilíbrio de momentos, onde a soma de todos os momentos em torno de deve ser nula:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força trativa T no parafuso tensor do sistema polia-cabio em termos da massa m do corpo que ele sustenta. Despreze a massa das polias e do cabo.

Alguns elementos do sistema de fazer gelo de um refrigerador estão mostrados na figura. (Um “cubo” tem a forma de um segmento cilíndrico!) Uma vez que o cubo congela e um pequeno aquecedor (não mostra

A polia A transfere um torque constante de 100Nm para uma bomba por intermédio de seu eixo em C . A força trativa no lado de baixo da correia vale 600N . O motor B tem uma massa de 100k g e gira no se

O homem empurra o cortador de grama a uma velocidade constante, com uma força P que é paralela ao plano inclinado. A massa do cortador, com o saco de grama preso a ele, é de 50k g e tem centro de mass

Se o bloco de 5k g é suspenso pela polia B e a curvatura da corda é d = 0,15m , determine a força na corda ABC. Despreze a dimensão da polia.