Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 17
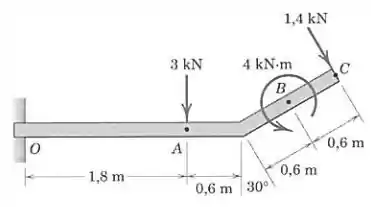
A viga uniforme tem massa de por metro de comprimento. Calcule as reações no apoio . As cargas mostradas estão em um plano vertical.
Passo 1
Adotando o sentido positivo para a direita, vamos descobrir a componente da reação no apoio por meio do equilíbrio na direção :
Isso significa que a força sobre a viga será para a esquerda.
Passo 2
Agora, trataremos do equilíbrio na direção , cujo sentido positivo será para cima.
Além das forças explícitas no desenho do enunciado, vamos considerar o peso da parte horizontal da viga, e o peso da parte inclinada da viga:
Assim, equacionamos o equilíbrio em , deixando todas as unidades em newtons:
Passo 3
Por último, somamos todos os momentos em torno de e igualamos a zero, para determinar o momento de reação. Lembre-se de que os pesos e atuam no ponto médio de cada parte da viga: