Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas Fundamentais - Ex. 2
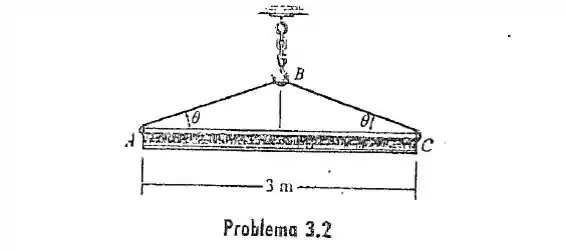
A viga tem um peso de 3,5 kN. Determine o cabo mais curto ABC que pode ser usado para levantá-la se a força máxima que o cabo pode suportar é .
Passo 1
Falaa!
Antes de qualquer exercício de estática devemos desenhar o diagrama de corpo livre.
Nessa caso vamos analiser a viga:
E podemos simplicar isso, mudando para uma situação equivalente, analisando o equiíbrio de forças nesse ponto:
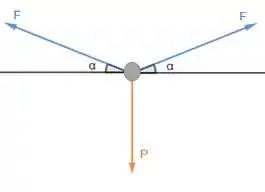
As forças são as mesmas forças que atuam na corda, ou seja elas não podem ser maiores que .
Para o cabo ser o mais curto possível, os ângulos, , devem ser os menores possíveis.
Passo 2
Como tudo isso ai tem que estar parado, a soma de forças em e em deve ser zero.
A soma das forças em realmente são zero:
Mas não conseguimos descobrir nada a partir delas.
Passo 3
Agora vamos decompor as forças em e montar a e equação para esse eixo:
Sabemos que é a força que atua sobre a corda e que ela não pode ultrapassar de , então vamos usar esse valor em para descobrirmos o ângulo mínimo que a corda pode fazer com a viga para que o cabo aguente.
Passo 4
Como temos o ângulo, podemos encontrar o tamanho mínimo da corda. Ela é essa linha azul de comprimento
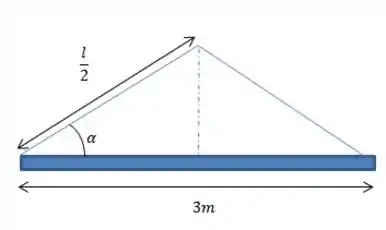
A partir do triângulo retângulo formado ali na esquerda, podemos dizer que:
Aquele ali, é referente a metade do comprimento da viga, que corresponde ao cateto adjacente do nosso triângulo... continuando