Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas Fundamentais - Ex. 3
Se o bloco de é suspenso pela polia B e a curvatura da corda é , determine a força na corda ABC. Despreze a dimensão da polia.
Passo 1
Fala, meu querido! Queremos a força na corda . Antes de qualquer exercício de estática devemos desenhar o diagrama de corpo livre.
Nessa caso vamos analiser a polia:
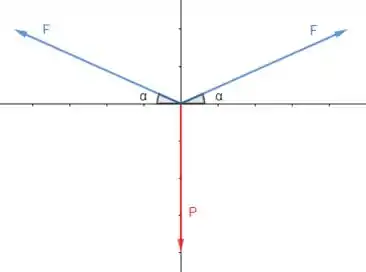
As forças são iguais, pois quando se solta a polia sobre a corda ela corre até um ponto de equilíbrio, que fica no centro da corda. E os ângulos também são iguais pelo mesmo motivo. Temos então uma simetria.
Passo 2
Como a polia não se meche, a soma de forças em e em deve ser zero.
Vamos decompor as forças em . Como , o ângulo que dá a direção delas, está colado em , nas duas decompomos multiplicando a força por cosseno. E como elas estão com sentidos contrários em relação a , ficam com sinais contrários.
Vemos que o somatório nesse eixo dá zero até nas cotinhas, por isso não conseguimos descobrir nada a partir delas.
Passo 3
Agora vamos decompor as forças em e montar a e equação para esse eixo. Como usamos cosseno na outra, aqui multiplicamos por seno para decompor nossas forças em . As duas apontam para cima, assim serão ambas positivas.
E repara que aqui aparece que é uma força somente no eixo . E como ela apontada para baixo, ela é negativa.
O peso do bloco é igual a sua massa vezes a gravidade:
Passo 4
Para descobrir falta achar .
A tangente do ângulo alfa pode ser descoberta através de relações trigonométricas:
Como temos as dimensão fornecidadas no enunciado e pela figura podemos falar que
Substituindo na equação: