Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 56
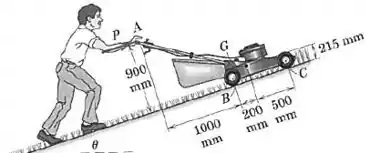
O homem empurra o cortador de grama a uma velocidade constante, com uma força que é paralela ao plano inclinado. A massa do cortador, com o saco de grama preso a ele, é de e tem centro de massa em . Se , determine as forças normais e sob cada par de rodas e . Despreze o atrito. Compare o resultado com as forças normais par as condições com e .
Passo 1
Vamos considerar os equilíbrios das forças nas duas direções e dos momentos das forças:
E aqui a direção é paralela ao plano inclinado, e é perpendicular ao plano.
Vamos começar com a direção , onde temos a força exercida pelo homem e uma componente do peso do cortador de grama:
Ena direção temos as duas normais e , e a outra componente do peso:
E agora vamos ver os momentos e relação ao ponto (escolhido por conveniência). Vamos colocar um sinal negativo nos momentos que favorecem rotação no sentido horário:
Passo 2
Agora vamos resolver esse conjunto de equações para encontrar as variáveis que queremos:
Substituindo alguns valores e reorganizando:
Substituindo a primeira equação na terceira:
E substituindo esse resultado na segunda equação:
Passo 3
Agora vamos considerar o caso em que e . Voltando ao nosso sistema:
Vamos trocar o por , e fazer :
E então:
Nesse caso, a terceira equação dá o seguinte resultado:
E substituindo isso na segunda equação:
Pronto!
Resposta
No caso em que : , e . No caso em que e : e .