Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 57

5.57. Os discos lisos D e E possuem um peso de 1   k N e 0,5   k N , respectivamente. Se uma força horizontal P = 1   k N é aplicada no centro do disco E, determine as reações normais nos pontos de contato com o solo em A, B e C.

Passo 1

Já vamos começar fazendo o diagrama de forças para o disco E

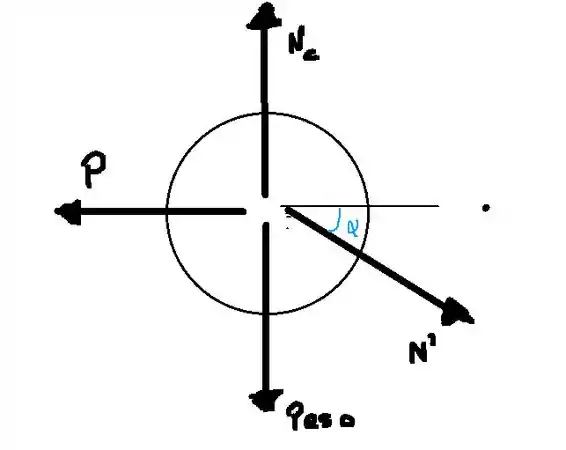
E aí temos as equações de equilíbrio

F R x = 0

F R x = - P + N ' ⋅ cos ⁡ α = 0

Podemos determinar cos ⁡ α   através da figura

cos ⁡ α = 24,91 5

Então

1 = N ' ⋅ 24,91 5

Então

N ' = 5 24,91 = 1,001   k N

E para y temos

F R y = 0

F R y = N c - 0,5 - N ' ⋅ sin ⁡ α = 0

Então

N c = 0,5 + 1,001 ⋅ 0,3 5 = 0,56   k N

Passo 2

Para o disco D temos

F R x = 0

F R x = N A ⋅ cos ⁡ θ - N ' 24,91 5 = 0

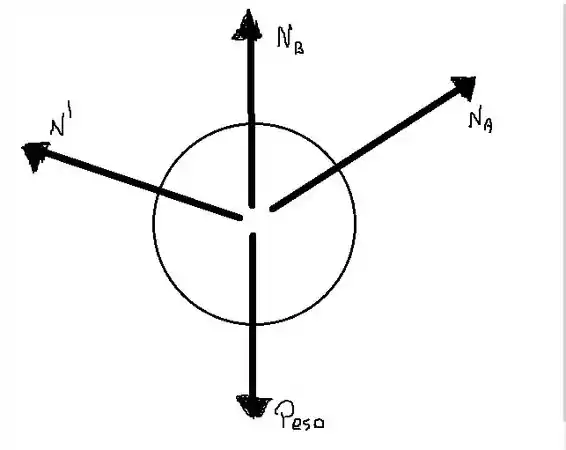
Podemos determinar cos ⁡ θ   através da figura

cos ⁡ θ = 4 5

N A ⋅ 4 5 = N ' 24,91 5

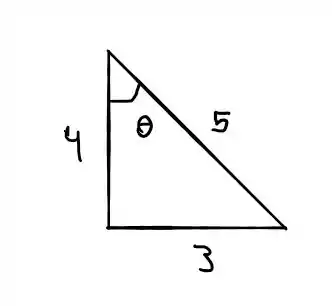
Então

N A = 1,001   24,91 5 ⋅ 5 4 = 1,25   k N

E para y temos

F R y = 0

F R y = N A ⋅ sin ⁡ θ + N B - 1 + N ' ⋅ sin ⁡ α = 0

Então

N B = - N A ⋅ sin ⁡ θ + 1 - N ' ⋅ sin ⁡ α

N B = - 1,25 ⋅ 3 5 + 1 - 1,001 ⋅ 0,3 5 = 0,19   k N

Resposta

N ' = 1,001   k N

N A = 1,25   k N

N B = 0,19   k N

N c = 0,56   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Exercício de Livro
Exercício de Livro
Exercício de Livro
Exercício de Livro
Se o bloco D pesa 1,5k N e o bloco B pesa 1,375k N , determine o peso do bloco C e do ângulo θ para o equilíbrio.