Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas Fundamentais - Ex. 1

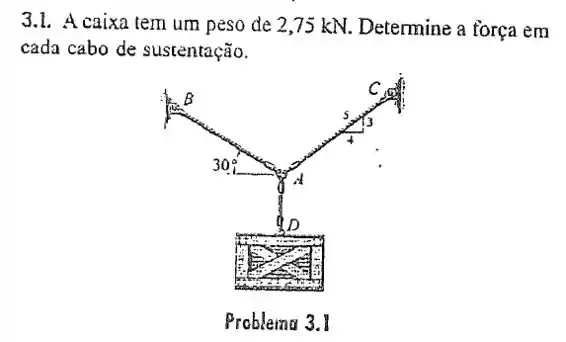
Passo 1

Antes de qualquer exercício de estática devemos desenhar o diagrama de corpo livre.

Nessa caso vamos analiser o nó A:

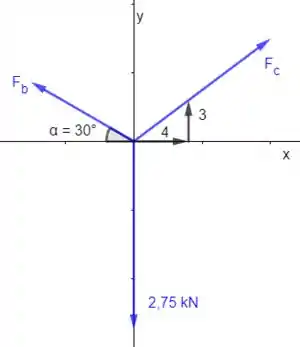
Passo 2

Como tudo isso ai tem que estar parado, a soma de forças em x e em y deve ser zero.

Vamos decompor as forças em x :

sum F_x = 0

F_c cos theta - F_b cos 30 = 0

Esse theta que eu coloquei na equação é o ângulo que o vetor F_b faz com o eixo x. A questão fez o desenho de um triângulozinho sob esse vetor, então podemos descobrir o cosseno do ângulo usando as relações trigonométricas.

cos theta = (C a t e t o a d j a c e n t e)/(H i p o t e n u s a)

cos theta = (4)/(5)

Continuando a equação:

(4 F_c)/(5) - (sqrt(3) F_b)/(2) = 0

(4 F_c)/(5) = (sqrt(3) F_b)/(2)

F_c = (5 sqrt(3) F_b)/(8) (1)

Passo 3

Agora vamos decompor as forças em y e montar a e equação para esse eixo:

sum F_y = 0

F_c s en theta + F_b s en 30 - 2,75 * 10^3 = 0

Esse theta que eu coloquei na equação, assim como antes, é o ângulo que o vetor F_b faz com o eixo x. Vamos descobrir o seno do ângulo usando, novamente, as relações trigonométricas.

s en theta = (C a t e t o o p o s t o)/(H i p o t e n u s a)

s en theta = (3)/(5)

Continuando a equação:

(3 F_c)/(5) + (F_b)/(2) - 2,75 * 10^3 = 0

Substituindo (1) nessa equação:

(3)/(5) ((5 sqrt(3) F_b)/(8)) + (F_b)/(2) = 2,75 * 10^3

Colocando F_b em evidência

F_b ((3 sqrt(3))/(8) + (1)/(2)) = 2,75 * 10^3

F_b ((3 sqrt(3) + 4)/(8)) = 2,75 * 10^3

F_b = 2,75 * 10^3 ((8)/(3 sqrt(3) + 4))

F_b = 2,39 * 10^3 N

Passo 4

Agora podemos usar a equação (1) para descobrir F_c :

F_c = (5 sqrt(3) F_b)/(8)

F_c = (5 sqrt(3) (2,39 * 10^3))/(8)

F_c = 2,59 * 10^3 N

Resposta

F_b = 2,39 k N

F_c = 2,59 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

96- A fim de obter a melhor distribuição de peso sob as quatro rodas da caminhonete de carga do Problema 6.95 , um tipo de fixação compensatória mostrada na figura é usada para a caminhonete rebocar o
98- Resolva o Problema 6.97 considerando que a carga de 75k N foi removida.
97- A cabine e a unidade motora da pá carregadeira articulada mostrada na figura estão ligadas por um pino vertical localizado 2m atrás das rodas da cabine. A distância de C para D é 1m . O centro de
125- Resolva o Problema 6.124 quando a )β = 0 , β = 6
124- A barra de comando C E passa através do mancal horizontal no corpo do sistema de alternância mostrado na figura. Sabendo que a haste de ligação B D tem comprimento de 250m m , determine a força Q