A barra delgada uniforme de ângulo reto tem massa . Se o atrito no pivô for desprezado, determine a magnitude da força normal em e a magnitude da reação do pino em .

Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!

O enunciado nos pede duas coisas:

i) Determinar o módulo da força normal ;

ii) Determinar o módulo da reação do pino em .

Então bora lá! Vamos começar fazendo um diagrama de corpo livre da barra , que será dividida em duas: e . Nele vamos expressar todas as forças atuantes no sistema: peso da barra , peso da barra , força normal no ponto de contato e as reações no pino .

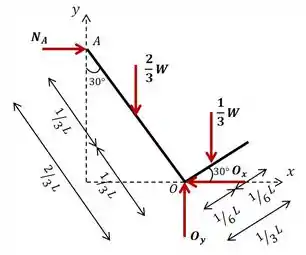
Para os nossos cálculos, vamos adotar que as forças são positivas quando estiverem nos sentidos positivos dos eixos (apontando para a direita em e para cima em ). Já os momentos serão considerados positivos quando estiverem no sentido anti-horário e negativos no sentido horário.

Nosso problema possui três incógnitas: , e . Para determina-las precisamos das duas equações de equilíbrio de forças (eixos e ) e a equação de equilíbrio do momento (eixo ). O pulo do gato aqui é escolher com qual equação de equilíbrio começar. Como as reações e estão sendo aplicadas exatamente neste ponto, elas não produzem momento ao redor dele, nos restando apenas como incógnita.