Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 58
Para a situação descrita na Fig. P2.47, determine o valor de para que a tensão na corda BC seja a menor possível, o valor correspondente dessa tensão.
Passo 1
Tá legal, vamos lá! Antes de começar o exercício, é sempre bom ter em mente as dicas que o próprio livro nos dá antes de cada seção de exercícios, na parte de “metodologia para resolução de problemas”. Então beleza, seguindo aquelas dicas, vamos começar fazendo o diagrama de corpo livre:
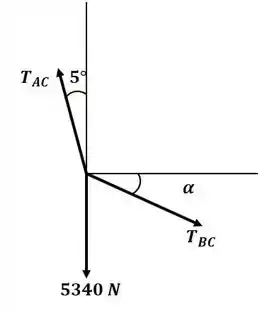
Passo 2
Agora que temos o DCL do problema, e temos somente três forças, vamos desenhar o triângulo de forças do sistema para descobrir os valores das tensões.
E aí vem o pulo do gato... Repara na figura a seguir:
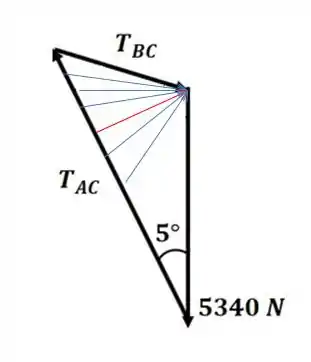
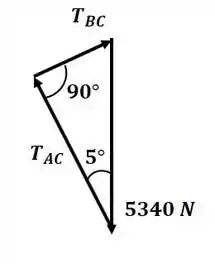
Conforme a gente vai mudando o , a gente vai mudando o ântulo entre e . Repara que vai diminuindo (só olhar o tamanho do vetorzinho que representa) até chegar em um ponto que vai ser mínima, que vai ser quando fazem 90°, sacou???
Repara no DCL, como fica (com umas linhas paralelas e tals):
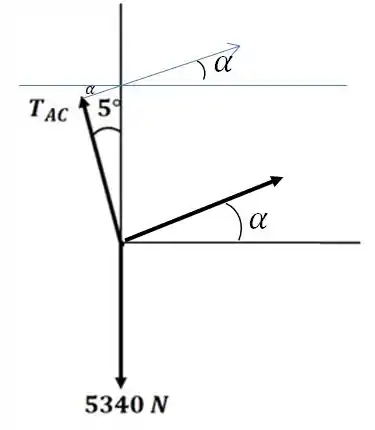
Agora vamos pegar esse recorte aqui, com calma:
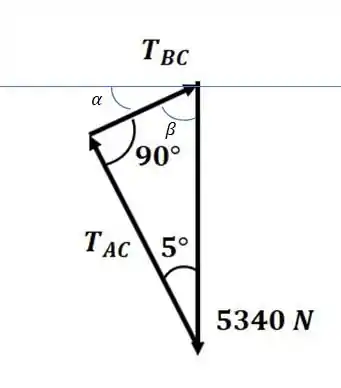
Se liga só... Como os ângulos internos do triângulo têm que somar 180°:
E também a gente pode tirar que:
Passo 3
Agora podemos relacionar o valor através do triângulo de forças do passo 2, que é um triângulo retângulo: