Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 38

3.38. O peso de 5   k g é suportado pela corda AC, pelo rolete, e por uma mola. Se a mola possui um comprimento não deformado de 200   m m . Determine a distância d até onde o peso está localizado quando em equilíbrio.

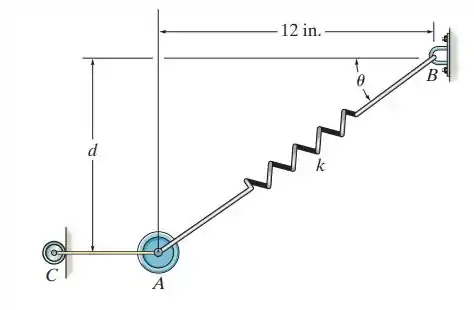
Passo 1

Vamos usar as equações de equilíbrio, começando por y

F R y = 0

F R y = F k ⋅ sin ⁡ θ - 49,05 = 0

F k ⋅ sin ⁡ θ = 49,05

Esse F k é a força da mola

Passo 2

Vamos calcular F k agora

F k = k ⋅ x

Esse x é a distância que a mola se move

Repare no triângulo para determinar essa distância

F k = k 300 cos ⁡ θ - 200

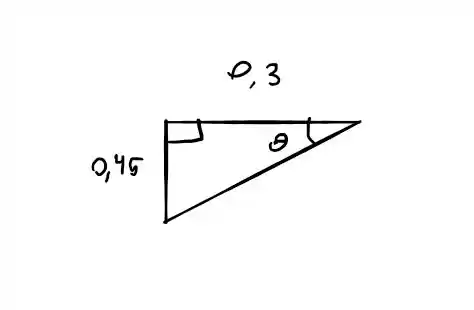
E pelo mesmo triângulo podemos determinar θ, assim

tan ⁡ θ = 3 2

Então

θ = 53,3 °

Assim teremos

F k = k 300 cos ⁡ 53,3 ° - 200

Passo 3

Agora podemos usar a equação de equilíbrio

F k ⋅ sin ⁡ θ = 49,05

k 300 cos ⁡ 53,3 ° - 200 ⋅ sin ⁡ 53,3 ° = 49,05

k = 49,05 300 cos ⁡ 18,435 ° - 200 ⋅ sin ⁡ 18,435 ° = 0 , 1795   N / m m

Resposta

k = 0,1795   N / m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para cada uma das placas e carregamentos mostrados nas figuras, determine as reações em A e B.
A barra AB, articulada em A e presa em B ao cabo BD, suporta as cargas mostradas nas figuras. Sabendo que d = 15 0m m , determine ( a ) a tração no cabo BD, ( b ) a reação em A.
63. Usando o método da Seção 4.7 , resolva o Problema 4.17
64. Usando o método da Seção 4.7 , resolva o Problema 4.18 .
61. Determine as reações em A e B quando a = 180m m