Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 63
63. Usando o método da Seção , resolva o Problema
Passo 1
Para começar a ver como resolver esse problema, vamos analisar o diagrama de corpo livre do nosso sistema.
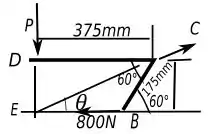
Olhando esse diagrama podemos tirar o seguinte esquema, que vai nos facilitar a vida.
Então podemos determinar o ângulo com uma trigonometria bem maneira, assim:
Tendo o valor de podemos achar a força que atua em e a força que atua em , através das seguintes relações trigonométricas:
Passo 2
Vamos determinar a força que atua em .
Passo 3
Agora vamos determinar a força em .
Resposta
Exercícios de Livros Relacionados
Desprezando o atrito e o raio da polia, determine ( a) a tração no cabo ADB, (b) a reação em C.
O suporte em forma de T mostrado na figura é suspenso por uma pequena roda em E e por cavilhas em C e D. despresando o efeito do atrito, determine as reações em C, D e E quando θ=30°.
O suporte em forma de T mostrado na figura é apoiado por uma pequena roda em E e por cavilhas em C e D. despresando o efeito do atrito, determine (a) o menor valor de θ para que seu equilíbrio seja ma
Sabendo que a polia tem um raio de 0.5 m , determine os componentes das reações em A e E .
A chave inglesa especial para encanadores mostrada na figura é utilizada em espaços exíguos (por exemplo, sob um lavatório ou pia). Consiste essencialmente em um mordente B C articulado em B a uma has