Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 43

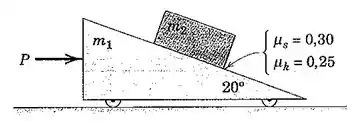
3/43) Determine a faixa de variação da força aplicada P para a qual o bloco de massa m 2 não escorregará sobre o bloco em formato de cunha de massa m 1 . Despreze o atrito associado com as rodas do bloco inclinado .

Passo 1

Então galera , primeiro bora organizar os dados que já conhecemos :

μ s = 0,30 μ k = 0,25 θ = 20 °

Analisando as forças que atuam na direção dos eixos x e y , temos que :

∑ F x = m a x   :   - F cos ⁡ θ + N sen ⁡ θ = m 2 a ∑ F y = 0   : F sen ⁡ θ + N cos ⁡ θ - m 2 g = 0

Resolvendo esse sitema de equações , obtemos que :

F = m 2 g sen ⁡ θ - a cos ⁡ θ N = m 2 a sen ⁡ θ + g cos ⁡ θ

Passo 2

Para impedir que o bloco deslize , temos que (usamos o coeficiente de atrito ESTÁTICO , pois supomos que não há movimento ) :

F = μ s N

Substituindo os valores de F e N que achamosno passo anterior :

m 2 g sen ⁡ θ - a cos ⁡ θ = μ s m 2 a sen ⁡ θ + g cos ⁡ θ

Sendo assim ,

a = g sen ⁡ θ - μ s cos ⁡ θ cos ⁡ θ + μ s sen ⁡ θ

Para θ = 20 ° e μ s = 0,30 :

a = 0,0577   g

Passo 3

Bom pessoal para acharmos a força máxima P aplicada para que o bloco m 2 não escorregue , inverteremos o sentido de F no diagrama de forças e obteremos a relação :

a = g sen ⁡ θ + μ s cos ⁡ θ cos ⁡ θ - μ s sen ⁡ θ = 0,745   g

E para determinarmos a faixa de variação da força aplicada P para a qual o bloco de massa m 2 não escorregará , usaremos afórmula :

∑ F x = m a x   : P = m 1 + m 2 a

Então ,

0,0577 m 1 + m 2 g ≤ P ≤ 0,745 m 1 + m 2 g

Resposta

0,0577 m 1 + m 2 g ≤ P ≤ 0,745 m 1 + m 2 g

De boa galera? Bora fazer mais exercícios então!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elevador desce a partir do repouso com uma aceleração de m/s2 até alcançar uma velocidade de 4,5m / s . Determine o tempo exigido e a distância percorrida.
Um carro tem uma velocidade inicial de 25 m/s e uma desaceleração constante de 3m / s 2 . Determine a velocidade do carro quando t = 4s . Qual é o deslocamento do carro durante o intervalo de tempo de
O carro A parte do repouso em t = 0 e move-se ao longo de uma estrada reta com uma aceleração constante de 2m / s 2 até alcançar uma velocidade de 27m / s . Depois disso, ele mantém essa velocidade. Q
Uma partícula move-se ao longo de uma linha reta com uma velocidade v = 12 - 3 t 2m / s , onde t é dado em segundos. Quando t = 1s , a partícula está localizada 10m à esquerda da origem. Determine a a
Uma partícula move-se ao longo de uma trajetória em linha reta de tal maneira que em 4 s ela se move de uma posição inicial s a = - 8m para uma posição s b = + 3m . Então, em mais 5 s, ela move-se de