Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 48

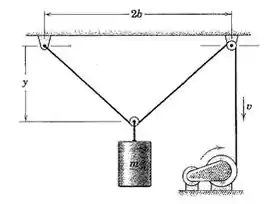
3/48) O tambor motorizado gira no sentido horário a uma velocidade constante . produzindo no cabo vertical uma velocidade constante v para baixo . Como parte do projeto deste sistema , determine a tração T no cabo em termos da coordenada y do cilindro de massa m . Despreze o diâmetro e a massa das pequenas polias .

Passo 1

Então galera, primeiramente vamos fazer a análise do somatório das forças que atuam sobre o bloco :

Temos duas forças de tração inclinadas atuadno sobre o bloco , portanto :

∑ F = m a   : 2 T   c o s θ - m g = m a

2 T   c a t e t o   a d j a c e n t e h i p o t e n u s a - m g = m a

2 T y y 2 + b 2 - m g = m a

a = - y "

Isolando T na equação , achamos que :

T = m a + g b 2 + y 2 2 y   o n d e   a = f ( v , y )

Além disso , usando Pitágoras, achamos que :

L = c o m p r i m e n t o   do cabo A B C = 2 b 2 + y 2

Passo 2

Bom pessoal , agora derivamos a equação do comprimento do cabo encontrada no passo anterior para acharmos arelação das velocidades :

- v = L ' = 2 y y ' b 2 + y 2

Usando um raciocínio análogo , se derivarmos a equação das velocidades , encontramos uma relação para as acelerações :

L " = 2   b 2 + y 2 y ' 2 + y y ' b 2 + y 2 - 2 ( y y ' y y ' b 2 + y 2 b 2 + y 2 = 0

Sendo assim , temos que :

b 2 + y 2 ( v 2 b 2 + y 2 4 y 2 + y y " ) = y 2 b 2 + y 2 v 2 b 2 + y 2 4 y 2

Isolando y " e simplificando obtemos que :

y " = - b 2 v 2 4 y 3 = - a

Portanto ,

T = m g + b 2 v 2 4 y 3 b 2 + y 2 2 y

T = m 2 y b 2 + y 2 g + b 2 v 2 4 y 3

Resposta

T = m 2 y b 2 + y 2 g + b 2 v 2 4 y 3

Tranquilo pessoal? Então partiu resolver mais questões

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula está se movendo ao longo de uma trajetória reta. Se a sua posição ao longo do eixo x é x = ( 8 t ) m , onde t é dado em segundos, determine sua velocidade escalar quanto t =2 s .
Uma partícula é forçada a se mover ao longo da trajetória. Se x = ( 4 t 4 ) m, onde é dado em segundos, determine a intensidade da velocidade e da aceleração da partícula quanto t = 0,5 s.
12.82 Um carro desloca-se 2 km para leste por 5 minutos em seguida, 3 km para norte por 8 minutos em seguida, 4 km para oeste por 10 minutos. Determine a distância total percorrida e a intensidade do
39. Levando em consideração a variação da aceleração gravitacional a com relação à altitude y ( ve Problema 12.38), deduza uma equação que relacione a velocidade de uma partícula caindo livremente com
29. A posição de uma partícula ao longo de uma linha reta é dada por s = 1,5 t 3 - 13,5 t 2 + 22,5 tm , onde t é dado em segundos. Determine a posição da partícula quando t = 6 s e a distância total q