Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 71

Um avião de 5 Mg está voando com uma velocidade constante de 350 km/h ao longo da trajetória circular horizontal. Se o ângulo de inclinação θ = 15 ° , determine a força de sustentação L atuando sobre o avião e o raio r da trajetória circular. Despreze a dimensão do avião.

Passo 1

A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.

Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:

a n = v 2 ρ

Passo 2

Vamos começar por esboçar o diagrama de corpo livre do nosso problema. Desta forma, temos:

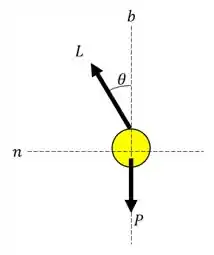
Temos apenas a ação de duas forças: peso e a de sustentação. A força de sustentação deve ser suficientemente grande para que ela consiga contrabalancear a força peso na direção b e produza uma aceleração na direção normal para manter a trajetória curvilínea!

Passo 3

Vamos começar descobrindo qual é o valor da força L. Para isto, precisamos fazer o somatório das forças na direção b, uma direção que o corpo não está sujeito a nenhuma acelera��ão! Portanto, temos

∑ F b = m ⋅ a b = 0

L ⋅ cos ⁡ θ - P = 0

L ⋅ cos ⁡ θ = m g

L = m g cos ⁡ θ = 5 ⋅ 10 6 ⋅ 9,81 cos ⁡ 15 °

L = 50,78   k N

Passo 4

Agora que descobrimos a força de sustentação, precisamos descobrir o raio de curvatura. Para isto, vamos analisar o somatório de forças na direção normal a trajetória. Temos então:

∑ F n = m ⋅ a n = m v 2 r

L ⋅ sen ⁡ 15 ° = m v 2 r

50,78 ⋅ 10 3 ⋅ sen ⁡ 15 ° = 5 ⋅ 10 6 ⋅ 350 3,6 2 r

r = 3596,9   m

Resposta

L = 50,78   k N

r = 3596,9   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de massa m é guiada ao longo da trajetória circular vertical r = 2 r c cos ⁡ θ usando o braço O A . Se o braço tem velocidade angular constante θ ˙ 0 determine o ângulo θ ≤ 45 ° no qual a bol
Um garoto parado firmemente em pé gira a garota sentada em um ‘prato’ circular ou trenó em uma trajetória circular de raio r 0 = 3 m de tal maneira que sua velocidade angular é θ ˙ 0 = 0,1 rad/s. Se o
A partícula lisa tem massa de 80 g. Ela está ligada a uma corda elástica estendendo-se de O a P e, devido ao braço de guia ranhurado, desloca-se ao longo da trajetória circular na horizontal r = 0,8 s
O cilindro C de 1,5 kg desloca-se ao longo da trajetória descrita por r = ( 0,6 sen ⁡ θ ) m. Se o braço está girando O A no sentido anti-horário com uma velocidade angular de θ ˙ = 3 rad/s, determine
O tubo gira no plano horizontal com uma taxa constante de θ ˙ = 4r a d / s . Se a bola B de 0,2 kg parte da origem O com uma velocidade radial inicial de r ˙ = 1,5m / s e se movimenta para fora do tub