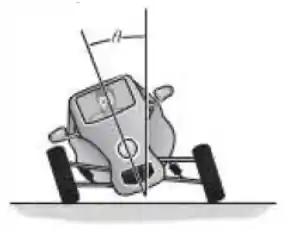
Um veículo é projetado para combinar a sensação de uma motocicleta com o conforto e a segurança de um automóvel. Se o veículo está se movendo a uma velocidade constante de 80 km/h ao longo de uma estrada circular curva de raio 100 m, determine o ângulo de inclinação do veículo de maneira que somente uma força normal do assento atue sobre o motorista. Despreze a dimensão do motorista.

Vamos começar por esboçar o diagrama de corpo livre. Considerando a pessoa como uma partícula, temos o seguinte diagrama:

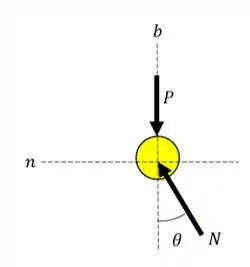
Como requisitado pelo problema, precisamos determinar uma inclinação para que, no somatório das forças, apenas a força normal atue sobre o motorista. Pelo diagrama, percebemos que também há uma força peso.

Portanto, a força normal deve contrabalancear a força peso na direção b. Desta forma, a resultante do somatório destas forças será a componente na direção normal da força normal.

Vamos descobrir a relação da força normal com a força peso. Para isto, façamos o somatório das forças na direção b, perpendicular ao plano da trajetória do carro. Desta forma,

Agora, vamos fazer o somatório das forças na direção normal. Portanto,