Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 110

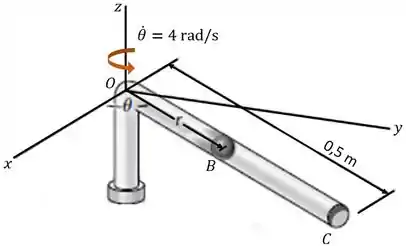
O tubo gira no plano horizontal com uma taxa constante de θ ˙ = 4   r a d / s . Se a bola B de 0,2 kg parte da origem O com uma velocidade radial inicial de r ˙ = 1,5   m / s e se movimenta para fora do tubo, determine as componentes radial e transversal da velocidade da bola no instante que ela deixa a extremidade do tubo em C , r = 0,5 m. Dica: mostre que a equação do movimento na direção r é r ¨ - 16 r = 0 . A solução é da forma r = A e - 4 t + B e 4 t . Avalie as constantes de integração A e B e determine o tempo t quando r = 0,5 m. Proceda para obter v r e v θ .

Passo 1

O Problema nos deu as seguintes informações:

Massa da bola: m = 0,2   k g

Velocidade angular constante: θ ˙ = 4 rad/s

Velocidade radial inicial: r ˙ = 1,5   m / s

Além disso, como a velocidade angular é constante,

d θ ˙ d t = θ ¨ = 0   r a d / s 2

Em seguida, é pedido encontrarmos os componentes radial e transversal da velocidade da bola no instante que ela deixa a extremidade do tubo em C , onde r = 0,5 m.

Vamos começar a resolver a questão utilizando a dica dada.

Passo 2

Primeiramente, vamos mostrar que a equação do movimento na direção r é r ¨ - 16 r = 0 .

Sabemos que

∑ F r = m a r

a r = r ¨ - r θ ˙ 2

Unindo estas duas fórmulas, obtemos

∑ F r = m ( r ¨ - r θ ˙ 2 )

Como não há forças externas sendo aplicadas à bola,

m r ¨ - r θ ˙ 2 = 0

Substituindo θ ˙ = 4 rad/s na equação acima, obtemos

r ¨ - r 4 2 = 0

r ¨ - 16 r = 0

A equação encontrada é uma Equação Diferencial homogênea de 2a ordem.

Passo 3

Em seguida, iremos encontrar a solução para esta equação.

Assumimos que r ¨ = y 2 , r ˙ = y e r = 1 ,

y 2 - 16 = 0

y 2 = 16

y = ± 4

Portanto, as raízes da Equação Diferencial, são y 1 = - 4 e y 2 = 4 .

Como as raízes são reais e distintas entre si, a equação pode ser escrita como

r = A e y 1 t + B e y 2 t

r = A e - 4 t + B e 4 t

Agora precisamos encontrar os valores de A e de B . Para isso, devemos utilizar as condições iniciais.

Em t = 0 , r = 0 e r ˙ = 1,5 . 0 = A e 0 + B e 0

0 = A + B

Derivamos r e encontramos:

r ˙ = - 4 A e - 4 t + 4 B e 4 t

Substituindo novamente os valores das condições iniciais:

1,5 = - 4 A + 4 B

1,5 4 = - A + B

Em seguida, resolveremos o sistema:

0 = A + B 1,5 4 = - A + B

Obtemos os seguintes valores para A e B :

A = - 0,1875

B = 0,1875

Logo,

r = - 0,1875 e - 4 t + 0,1875 e 4 t

Passo 4

Em seguida, o enunciado diz para determinarmos o tempo t quando r = 0,5 m

Logo,

0,5 = - 0,1875 e - 4 t + 0,1875 e 4 t

0,5 0,1875 = - e - 4 t + e 4 t

Para conseguir resolver esta parte, devemos lembrar das funções hiperbólicas, onde

senh ⁡ t = e t - e - t 2

cosh ⁡ t = e t + e - t 2

Voltando a resolução, dividiremos ambos os lados por 2:

0,5 0,1875 ( 2 ) = - e - 4 t + e 4 t 2

Podemos ver que o resultado do lado direito é igual ao senh ⁡ 4 t , portanto

senh ⁡ 4 t = 0,5 0,1875 ( 2 ) = 1,33

4 t = senh - 1 ⁡ 1,33

t = senh - 1 ⁡ 1,33 4

t = 0,275   s

Passo 5

Sabemos que v t = r ˙ e v θ = r θ ˙ .

Para t = 0,275   s :

r = 0,5   m

θ ˙ = 4   r a d / s

Precisamos encontrar r ˙ .

r ˙ = - 4 A e - 4 t + 4 B e 4 t

r ˙ = - 4 ( - 0,1875 ) e - 4 0,275 + 4 ( 0,1875 ) e 4 ( 0,275 )

r ˙ = 2,50   m / s

Logo,

v t = r ˙ = 2,50   m / s

v θ = r θ ˙ = 0,5 4 = 2   m / s

Resposta

v t = 2,50   m / s

v θ = 2   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3/59) As pequenas esferas são livres para se deslocar nasuperfície interna das câmaras esféricas rotativas rotativas mostradas em seção transversal com raio R = 200m m . Se as esferas atingem uma posi
3/51) Se o bloco de 2k g passa sobre o topo B da porção circular da trajetória com uma velocidade de 3,5m / s , calcule o módulo N B da força normal exercida pela trajetória sobre o bloco . Determine
3/55) O carro passa sobre o topo de uma curva num plano vertical em A com uma velocidade de 60k m / h e então passa pelo fundo de uma depressão em B . Os raios de curvatura da estrada em A e B são amb
3/57) O tubo vazado em torno do eixo horizontal que passa pelo ponto O e girano plano vertical com umavelocidade angular constante no sentido anti-horário θ ' = 3 r a d / s . Se uma partícula de 0,1k
3/63) Quando o esqueitista transpõe asuperfície mostrada , as velocidades do seu centro de massa em θ = 0 ° , 45 ° e 90 ° são 8,5m / s , 6m / s e 0 , respectivamente . Determine a força normal entre a