Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 7
A haste é feita de aço com 25 mm de diâmetro. Determine a carga crítica de flambagem, se as extremidades estiverem apoiadas em roletes., .
Passo 1
Esse é um problema bem direto sobre flambagem, que é quando uma barra enverga por causa da ação de forças axiais. Para resolver a gente tem que lembrar principalmente da nossa equação de flambagem:
Onde:
- é a força crítica (força máxima que a barra aguenta antes do escoamento).
- é o coeficiente de elasticidade do mateiral.
- é o nosso coeficiente de flambagem.
- é o comprimento efetivo.
- é o momento de inércia.
O problem pede exatamente e nos fornece o , o e o diâmetro que utilizaremos para calcular o momento de inércia .
Então para resolver essa questão a gente tem que, além de calcular o momento, encontrar o coeficiente de flambagem . Para, desta forma, encontrar a força crítica.
Depois de achar a força crítica a gente vai poder achar a tensão normal que essa força gera na barra e comparar com a tensão de escoamento fornecida .
Então vamos lá?
Passo 2
Se liga só! A primeira coisa que temos de fazer, é verificar qual o comprimento efetivo de flambagem pra nossa haste...
O requisito básico pra que cada uma dessas situações aconteça, é o seguinte...
Para te ajudar segue uma imagem aqui. (nesse caso temos a viaga na vertical invés da horizontal, mas isso não faz muita diferença no final das contas).
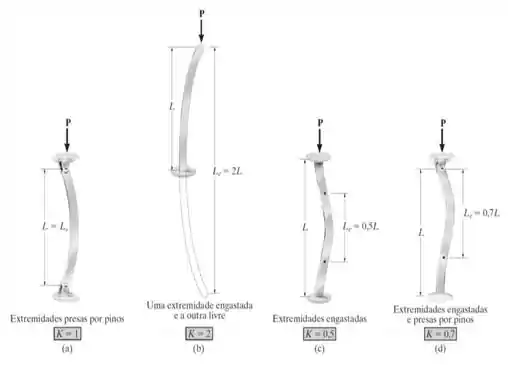
Como ambas as extremidades estão presas por roletes então temos:
Passo 3
Além disso, do enunciado também tiramos que...
Continuemos nosso raciocínio!
Vamos obter o valor de , que é a nossa carga crítica!
Para calcular isso falta só o momento de inércia . Como haste tem seção circular, o seu momento de inércia de é obtido do seguinte jeito abaixo...
Onde é o raio da seção... No caso, igual a...
Logo o momento de inércia vale:
Substituindo então os valores numéricos, chegamos até o valor da carga crítica...
Beleza, agora a gente tem que conferir também a tensão normal!
Passo 4
Agora vamos começar nosso teste...
A outra variável que queremos obter é a área da nossa seção transversal :
E como já temos os valores que precisávamos, substituindo eles na nossa fórmula da tensão crítica, obtemos que...
Passo 5
Chegou a hora da verdade! Bora pra comparação!
O valor da nossa tensão crítica é menor do que a tensão admissível para o nosso aço, igual a .
Isso significa que a barra não entrará em escoamento. Ai que alívio!
Então tá tudo certo! Haste ok! Carga crítica ok!
Concluímos então que o valor da carga crítica, atende as especificações do material da haste, e vai ser igual à...
Finalizamos aqui!
Até a próxima!