Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 92
O caminhão, inicialmente em repouso com um rolo de papel cilíndrico compacto na posição mostrada, se desloca para a frente com uma aceleração constante . Encontre a distância que o caminhão percorre antes que o papel role da borda de sua plataforma horizontal. O atrito é suficiente para evitar o deslizamento.
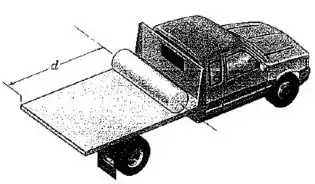
Passo 1
Vamos dizer que, no final das contas, a aceleração do centro de massa do rolo em relação ao solo é , na direção horizontal.
Então, pela segunda lei de Newton:
E a única força que age sobre o rolo nessa direção é a força de atrito , então:
Ainda temos duas variáveis desconhecidas ( e ), então precisamos de mais uma equação. Vamos olhar para a soma dos momentos em relação ao centro de massa:
E a única força que produz momento em relação ao centro de massa também é a força de atrito , ou seja:
Passo 2
Então ficamos com um sistema de duas equações:
E eliminando entre as duas equações e cortando :
E precisamos encontrar uma expressão para a aceleração angular do rolo. Isso pode ser um pouco confuso, então vamos com calma.
O caminhão se move para frente com em relação ao solo. E o centro de massa do rolo se move também para frente, com aceleração em relação ao solo.
Se você olhar de fora, vai ver o rolo se movendo em direção à traseira do caminhão. Isso acontece apesar de os dois estarem se movendo para frente, porque o caminhão tem um aceleração .
Então beleza, então como podemos escrever a aceleração angular do rolo?
Pense nessa diferença do numerador com o a aceleração da carroceria do caminhão em relação ao rolo. Em outras palavras, a aceleração com que o chão passa por baixo do rolo e faz ele girar.
Substituindo isso na nossa equação:
Passo 3
Agora podemos calcular a aceleração do centro de massa do rolo em relação ao caminhão:
E o sinal negativo indica que essa aceleração aponta para trás.
Com essa aceleração relativa, quanto tempo o rolo leva para percorrer a distância e cair do caminhão?
Beleza, agora podemos responder à pergunta final: qual a distância percorrida pelo caminhão até o rolo cair da carroceria?
É só calcular a distância percorrida pela aceleração no tempo que acabamos de determinar:
Resposta
O caminhão percorre uma distância .