Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.8 - Ex. 108

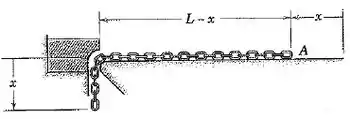
4/108) A corrente de comprimento L e massa ρ por unidade decomprimento é liberada a partir do repouso sobre a superfície horizontal lisa com uma parte desprezivelmente pequena pendurada x para iniciar o movimento . Determine (a) a aceleração a em função de x , (b) a tração T na corrente na borda lisacomo uma função de x , e (c) a velocidade do último elo A quando atinge a borda .

Passo 1

Então galera , para resolvermos este exercício , devemos lembrar que a equação de trabalho-energia é dada por :

U 1 - 2 ' = ∆ V g + ∆ T

E como o sistema é conservativo , sabemos que U 1 - 2 ' = 0 , sendo assim:

∆ V g + ∆ T = 0

Substituindo as relações para ∆ V g e ∆ T achadas nesta seção , obtemos que :

- ρ g x x 2 + 1 2 ρ L x ' 2 = 0

Isolando x ' na equação , achamos que :

g L x 2 = x ' 2

Logo ,

x ' = g L x

Para acharmos a aceleração , por sua vez , basta derivarmos a relação obtida acima :

a = x " = g L x ' = g L g L x  

Então ,

  a = g L x  

Passo 2

Bom pessoal , para obtermos uma função de x para a tração , aplicamos a equação de equilíbrio em relação ao sistema :

∑ F = m a   : T = ρ L - x g L x

Sendo assim , temos que :

T = ρ g x 1 - x L

Passo 3

Então pessoal , para acharmos a velocidade do último elo A , devemos lembrar da relação :

v d v = a x d x  

Integrando os dois lados da equação , obtemos que :

  ∫ 0 v v d v = g L ∫ 0 L x d x

Logo ,

v 2 2 = g L L 2 2

Isolando v na equação , achamos que :

v = g L

Resposta

a = g L x  

T = ρ g x 1 - x L

v = g L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um homem de 75 kg sobe a corda com uma aceleração de 0,25m / s 2 , medida em relação à corda. Determine a tração na corda e a aceleração do bloco de 80k g .
O eixo CA de 2 kg passa por um mancal radial liso em B. Inicialmente, as molas, que estão enroladas livremente em torno do eixo, não estão deformadas quando nenhuma força é aplicada ao eixo. Nesta pos
O bloco B tem massa m e é solto do repouso quando está no topo da carreta A que tem massa de 3m. Determine a tração na corda CD necessária para evitar que a carreta se desloque enquanto B escorrega pa
O bloco A de 5k g desloca-se para a direita com v A = 0,6m / s no instante mostrado. Se o coeficiente de atrito cinético entre a superfície e A é μ k = 0,2 , determine a velocidade de A quando ele se
Um elevador de carga, incluindo a sua carga, tem massa de 500 kg. Ele é impedido de girar devido aos trilhos e rodas montados nos seus lados. Quando t = 2s , o motor M enrola o cabo com uma velocidade