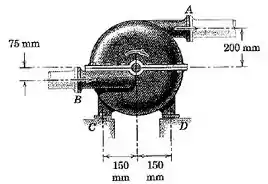
4/110) A bomba centrífuga processa de água doce por minuto com velocidades de entrada e de saída de . O impelidor gira no sentido horário através do eixo em acionado por ummotor que fornece a uma velocidade de bombeamento de . Com a bomba cheia , mas sem girar , as reações verticais em e são de cada uma . Calcule as forças exercidas pela fundação sobre a bomba em e enquanto a bomba está girando . As trações nos tubos conectado em e são precisamente equilibradas pelas respectivas forças devidas à pressão estática naágua . (Sugestão: Isole a bomba inteira e a água em seu interior entre as seções e e aplique o princípio da quantidade de movimento para o sistema completo.)

Bom pessoal , além disso , aprendemos neste capítulo que a resultante dos momentos em relação a deve ser igual a , a taxa de variação no tempo da quantidade de movimento angular do sistema, sendo assim :

Logo ,

Consequentemente , como as reações verticais em e com a bomba cheia , mas sem girar , são de cada uma , temos que ao girar :