Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 75
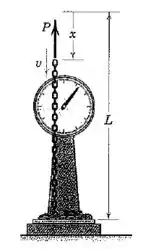
A extremidade superior da corrente de elos de comrpimento e massa por unidade de comprimento é abaixada a uma velocidade constante pela força . Determine a leitura da balança de plataforma em termos de .
Passo 1
Como a corda é abaixada a uma velocidade constante, é preciso que todas as forças estejam em equilíbrio.
Para que a força mantenha a velocidade constante (ou seja, não produza uma aceleração para cima), ela precisa equilibrar o peso da porção da corrente que ainda não está apoiada na balança:
Além da força peso, temos também a força peso da corrente (que não muda independente de estar apoiada ou não):
E além disso temos a força exercida pela balança, que é quem queremos medir.
Passo 2
Todas essas três são forças externas que agem sobre a corrente na direção vertical, então:
E vamos definir que o sentido positivo é vertical para baixo:
E substituindo na equação de cima:
Bom, agora vamos analisar esse termo da direita com cuidado. A velocidade da corrente é constante, então:
Mas a massa da porção da corrente que tem uma velocidade então:
Não esqueça que o ponto em cima da letra é só uma abreviação para o .
Passo 3
Então nossa equação fica assim:
Como e são constantes:
Mas é a própria velocidade de descida da corrente, então:
Agora é só isolar a força medida pela balança:
Resposta
A leitura da balança é dada por .