Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 24
Se a força do motor M sobre o cabo é mostrada no gráfico, determine a velocidade do carrinho quando . A carga e o carrinho têm massa de e o carrinho parte do repouso.
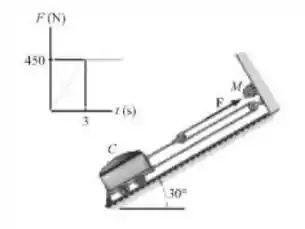
Passo 1
Temos um problema que envolve polias! Ao fazermos o corpo livre do nosso carrinho, precisamos considerar o efeito da força F sobre cada um dos trechos de corda. Como estamos relacionando forças com velocidades, aliaremos os nossos conhecimentos de cinemática com cinética!
Sendo assim, precisamos tomar um grande cuidado nesse problema! O carrinho está sujeito a uma força crescente. Entretanto, como ele parte do repouso , ele só começará a andar quando o somatório das forças for maior que a componente do peso! Portanto, precisamos descobrir o período do tempo em que isto ocorre!
Passo 2
Vamos começar fazendo o diagrama de corpo livre do nosso carrinho. Como temos três trechos de corda, temos:
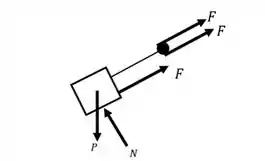
Como queremos analisar o deslocamento do carrinho ao longo do plano inclinado, temos:
Como a força é dada pela reta do gráfico, sabemos que , portanto,
Passo 3
Agora que descobrimos uma função para a aceleração, precisamos descobrir a partir de que tempo ela é positiva. Isto é, a partir de que tempo a força do motor consegue superar a componente do peso, fazendo com que o carrinho comece a se deslocar! Sendo assim, temos:
Portanto, o carrinho só será deslocado de até .
Passo 4
Agora que trabalhamos com a cinética, vamos voltar para a cinemática. Como obtemos a aceleração em função do tempo, basta integrarmos diretamente para obtermos a velocidade. Logo,