Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 109

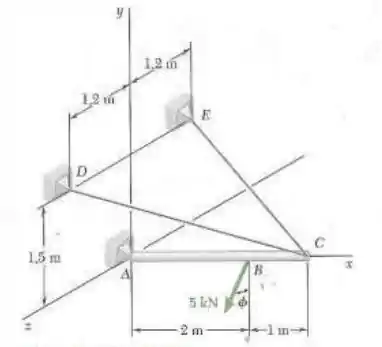
4.110. Uma viga de 3 m é mantida por uma rótula em A e pelos cabos CD e CE. Sabendo que a linha de ação da força de 5 kN atua verticalmente para baixo ϕ = 0 ° , determine (a) a tração nos cabos CD e CE, (b) a reação em A.

Passo 1

Vamos começar desenhando a situação

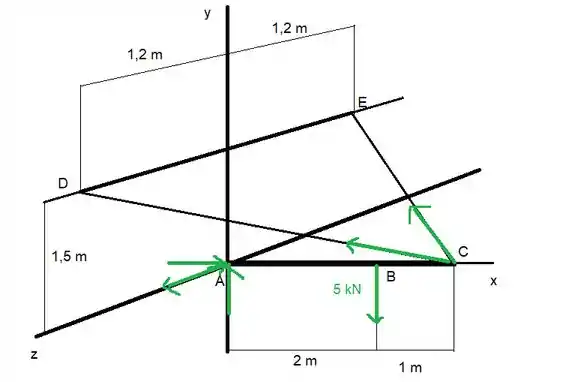
Aquelas forças ali perto do A são A x ,   A y   e   A z .

Pela simetria do problema, podemos ver que

T C D = T C E = T

Passo 2

A primeira coisa que vamos fazer é passar as tensões para notação vetorial, vamos precisar disso daqui a pouco, então é só multiplicar a tenção por seu vetor unitário.

T C D = T ⋅ C D → C D

Olha só

C D → = - 3   i ^ + 1,5 j ^ + 1,2   k ^  

E agora é só calcular seu módulo

C D → = C D = - 3 2 + 1,5 2 + 1,2 2 = 3,562

Então

T C D = T 3,562 - 3   i ^ + 1,5 j ^ + 1,2   k ^

E agora vamos usar o mesmo raciocínio para T C E

C E → = - 3 i ^ + 1,5 j ^ - 1,2 k ^

E seu módulo

C E → = C E = - 3 2 + 1,5 2 + - 1,2 2 = 3,562

Então

T C E = T 3,562 - 3   i ^ + 1,5 j ^ - 1,2   k ^

Passo 3

Agora vamos usar o momento no eixo A C -

∑ M A C = 0

r A C → × T C D → + r C A → × T C E → + r B A → × B → = 0

Vamos fazer isso parte por parte.

Começando por

r A C → × T →

r A C → = 3   i ^

Então

i ^ j ^ k ^ 3 0 0 - 3 1,5 1,2 ⋅ T 3,562

Por Laplace

r A C → × T → = T 3,562 - 3,6   j ^ + 4,5   k ^

Agora

r A C → × T →

r A C → = 3   i ^

Então

i ^ j ^ k ^ 3 0 0 - 3 1,5 - 1,2 ⋅ T 3,562

Por Laplace

r A C → × T → = T 3,562 3,6   j ^ + 4,5   k ^

E finalmente

r B A → × B →

r B A → = 2   i ^

Então

i ^ j ^ k ^ 2 0 0 0 - 5 0

Por Laplace

r B A → × B → = - 10   k ^

Agora é só somar tudo

T 3,562 - 3,6   j ^ + 4,5   k ^ + T 3,562 3,6   j ^ + 4,5   k ^ - 10 k ^ = 0

Passo 4

Como tudo é igual à 0, podemos separar as componentes e igualar à 0

Só precisamos da componente k ^

k : 2 3 ⋅ 1,5 ⋅ T 3,562 - 10 = 0

Logo

T = 3,958   k N

Passo 5

Ainda faltam 3 incógnitas, vamos usar a equação de equilíbrio para acha-las

∑ F = 0

A + T C D + T C E - 5 j ^ = 0

Agora separando por eixo

i ^ : - 2 3,958 ⋅ 3 3,562 = 0

Daqui a gente já tira

A x = 6,67   k N

Agora j

j ^ : A y + 2 3,958 ⋅ 1,5 3,562 = 0

Logo

A y = 1 , 667   k N

Agora finalmente

k ^ : A z = 0

Logo

A = 6,67   i ^ + 1 , 667   j ^ k N

Resposta

(a)

T C D = T C E = 3,96   k N

(b)

A = 6,67   i ^ + 1,667   j ^ k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a maior massa da caixa para que a tração desenvolvida em qualquer cabo não exceda 3k N .
Determine a tração desenvolvida nos cabos A B , A C e A D necessária para o equilíbrio da caixa de 150k g .
Determine a força em cada cabo para suportar a plataforma de 17,5 kN ( ≈ 1750k g ). Considere d = 0,6m .
Se a massa do vaso de planta é 50k g , determina a tração desenvolvida em cada fio para o equilíbrio. Considere x = 1,5m e z = 2m .
Se a massa do vaso é 50k g , determine a tração desenvolvida em cada fio para o equilíbrio. Considere x = 2m e z = 1,5m .