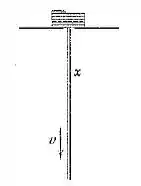
4/111) Substitua a corrente empilhada no Prob.4/92 por um rolo de corda de massa por unidade de comprimento e comprimento total como mostrado e determine a velocidade da seção em queda em termos de se acorda parte do repouso em . Mostre que a aceleração é constante em . A corda é considerda cmo sendo perfeitamente flexível em flexão , mas inextensível econstitui um sistema conservativo (sem perdade energia) . Os elementos dacorda adquirem sua velocidade de forma contínua a partir de zeró até em um pequeno trecho de transição da corda no topo do rolo . Para comparação com a corrente do Prob.4/92 , esta seção de transição pode ser considerada como tendo comprimento desprez´vel sem violar a exigência de que não haja perda de energia no presente problema . Determine também a força exercida pela plataforma sobre o rolo em termos de e explique por que se torna nula quando . Despreze as dimensões do rolo em comparação com .

Bom pessoal , como estudamos neste capítulo , a resultante de todas as forças externas deve ser igual a , a taxa de variação no tempo da quantidade de momento linear do sistema, sendo assim :

Logo ,

Consequentemente ,

Colocando em evidência :

Bom galera , analisando o problema para a seção vertical , temos que :

Logo ,

Isolando , achamos que :

Para um fluxo idealizado, um guia sem atrito deve ser introduzido. A guia e a bobina de comprimento são isoladas . Sendo assim , temos que ;

Logo ,

Isolando , achamos que :

Sendo assim , temos que quando .

Quando , por outro lado , a taxa de mudança de momento requer mais força do que , então reverte.