Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 17

Utilizando a notação da Seção 8.2 e desprezado o efeito das tensões de cisalhamento provocadas pela forças transversais, mostre que a tensão normal máxima em um eixo cilindro pode ser expressa como.

σ m á x = c J [ ( M y 2 + M c 2 ) 1 1 + ( M y 2 + M c 2 + T 2 ) 1 2 ] m á x

Passo 1

Começamos esboçando o diagrama e considerando que a tensão máxima de flexão é dada por:

σ m = M c I = M y 2 + M z 2 2 I = c J M y 2 + M z 2

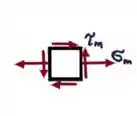
Tensão torcional máxima:

t m = T c J

σ m 2 = M y 2 + M z 2 c 2 I = c J M y 2 + M z 2

Passo 2

Usando o círculo de Mohr,

R = σ m 2 2 + t m 2 = c 2 j 2 ( M y 2 + M z 2 ) + T 2 c 2 J 2 = c J M y 2 + M z 2 + T 2

σ m á x i m o = σ m 2 + R = c J M y 2 + M z 2 + c J M y 2 + M z 2 + T 2

R = c J [ ( M y 2 + M z 2 ) 1 / 2 + ( M y 2 + M z 2 + T 2 ) 1 / 2 ]

Resposta

c J [ ( M y 2 + M z 2 ) 1 / 2 + ( M y 2 + M z 2 + T 2 ) 1 / 2 ]

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As cargas internas em uma seção da viga consistem em uma força axial de 500N , uma força de cisalhamento de 800N e duas componentes de momento 30N ⋅ m e 40N ⋅ m . Determine as tensões principais no po
As tensões principais em um ponto são mostradas na figura. Se o material for alumínio, para o qual E a l = 70G P a e v a l = 0,33 , determine as deformações principais.
As cargas internas que agem sobre uma seção transversal no eixo de acionamento de uma turbina de 150 mm de diâmetro consistem em uma força axial de 12,5 kN, um momento fletor de 1,2 kN.m e um momento
Um material está sujeiro às tensões principais σ x e σ y . Determine a orientação θ de um extensômetro coloca em um ponto, de modo que sua leitura da deformação normal responda apenas a σ y e não a σ
As cargas internas que agem sobre uma seção transversal no eixo de acionamento de uma turbina de 150 mm de diâmetro consistem em uma força axial de 12,5 kN, um momento fletor de 1,2 kN.m e um momento