Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 84
O eixo cônico está confinado pelos apoios fixos em e . Se for aplicado um torque em seu ponto médio, determine as reações nos apoios.
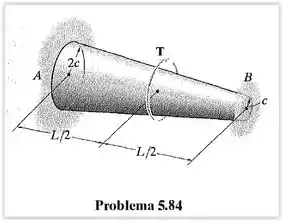
Passo 1
Vamos lá resolver esse problema?
O enunciado pede que encontremos o torque nos apoios e . O eixo cônico está fixo nas duas extremidades, então fazendo o diagrama de corpo livre e o somatório dos momentos, temos:
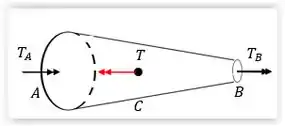
Fazendo um corte na seção , vemos que o único torque agindo é .
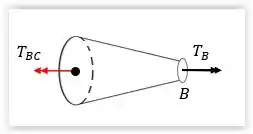
E fazendo um corte na seção , temos que:
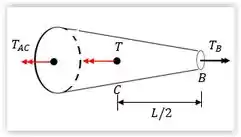
Passo 2
Vamos então desenhar um diagrama do corte lateral do eixo:
Fazendo uma semelhança de triângulos, temos que:
Com base no desenho, vamos então calcular o raio do eixo no local onde o torque é aplicado e chama-lo de :
Substituindo :
Passo 3
Vamos chamar de o ângulo que varia desde a extremidade até e de o que varia de até a extremidade . Observe que estamos pegando intervalos das extremidades ao ponto onde é aplicado!
É uma viga engastada nas duas extremidades, então:
Substituindo :
Aplicando a integração por substituição
Aplicando a integração por substituição :
Aplicando a regra da potência:
Simplificando, temos que:
Substituindo na expressão que encontramos no somatório: