Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 88
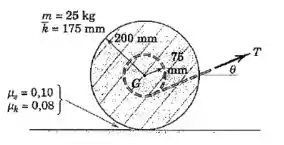
O disco circular com raio de possui uma massa de com raio de giração centroidal e possui uma ranhura circular concêntrica, com raio de , cortada nele. Uma força constante é aplicada, em um ângulo , ao cabo enrolado em torno da ranhura como mostrado. Se , , e , determine a aceleração angular do disco, a aceleração do seu centro de massa , e a força de atrito exercida pela superfície no disco.
Passo 1
Vamos começar desenhando um diagrama da situação no caso em que :
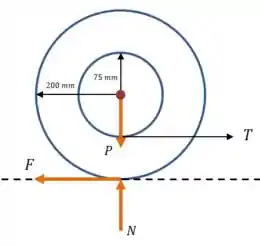
Agora vamos aplicar a segunda lei de Newton nas direções horizontal e vertical:
E então:
E agora vamos analisar o momento resultante em relação ao centro de massa:
Onde é o raio de giração.
Passo 2
E então ficamos com um sistema de três equações:
E podemos escrever uma equação extra se considerarmos que o disco rola sem deslizar:
E nosso objetivo é encontrar , e , de forma que não precisamos da primeira equação, então:
Vamos substituir os valores numéricos:
Vamos multiplicar a primeira equação por e somar com a segunda:
E agora substituindo com a terceira equação:
E podemos substituir isso na terceira equação para calcular :
E podemos substituir isso na primeira equação para calcular:
Passo 3
Agora só precisamos verificar se a nossa condição de rolamento sem deslizamento era razoável.
Já que o coeficiente de atrito estático é , então a força de atrito máxima que pode existir entre o disco e o plano é:
E essa força é superior a , então a nossa suposição é razoável.
Resposta
, e .