Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 62
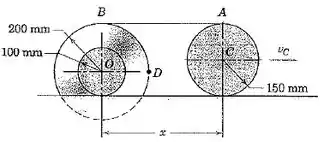
5/62) O centro da roda menor possui uma velocidade m/s na direção mostrada . O cabo que liga as duas rodas está firmemente enrolado em torno das respectivas periferias e não desliza . Calcule a velocidade do ponto quando está na posição mostrada . Calcule também a variação que ocorre por segundo quando é constante .
Passo 1
Então galera , como indicado na figura do problema , sabemos que :
Além disso , pelas relações aprendidas nesta seção , temos que :
Sendo assim ,
Passo 2
Bom pessoal , analisando o ponto , por sua vez , temos que :
Além disso , como demonstrado neste capítulo :
Logo ,
O módulo de , portanto , é dado por :
Sendo assim , temos que :
Resposta
Exercícios de Livros Relacionados
5/68) A placa quadrada uniforme se desloca no plano x y e possui uma velocidade angular no sentido horário . No instante representado , o ponto A tem uma velocidade de 2 m / s para a direita , e a vel
5/65) As duas polias são rebitadas em conjunto para formar uma única unidade rígida , e cada um dos dois cabos está firmemente enrolado em torno de suas respectivas polias . Se o ponto A no cabo de el
5/67) A roda de raio r rola sem deslizar e possui uma velocidade angular ω . Escreva uma expressão para a velocidade do ponto A em termos de θ e mostre que as velocidades de A e B são perpendiculares
5/59) A extremidade A da haste possui a velocidade indicada no instante representado . A extremidade B está confinada a se deslocar na ranhura. Para esse instante calcule a velocidade de B e a velocid
5/63) Por um curto intervalo , os cursores A e B estão deslizando ao longo do eixo fixo vertical com velocidade v A = 2 m / s e v B = 3 m / s nos sentidos indicados . Determine o módulo da velocidade