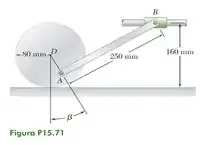
A roda de 80 mm de raio mostrada na figura rola para a esquerda com uma velocidade de 900 mm/s. Sabendo que a distância AD é 50 mm, determine a velocidade do cursor e a velocidade angular da barra AB quando (a) e (b) .
Passo 1
a) Bora pra questão 71 agora, meus caros (as)!
Bom! Temos que determinar a determine a velocidade do cursor e a velocidade angular da barra AB conforme varia o ângulo
Pois muito bem! Antes de qualquer coisa, vamos a algumas convenções...
Primeiro o sentido de rotação... Normalmente costumamos chamar o sentido horário de negativo e o sentido anti-horário de positivo.
Continuando nosso raciocínio, bora fazer um esboço do nosso sistema destacando os vetores posição de nosso interesse... Primeiro bora fazer o esboço de quando temos um ângulo
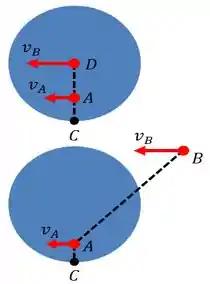
Como podemos ver na figura acima, em a velocidade é nula...
E em , a velocidade é dada, como podemos ver pelo enunciado, por...
Passo 2
Pronto! As informações mais importantes, já temos em mãos!
E uma vez que sabemos o valor de , temos que a velocidade angular da roda será de...
No sentido anti-horário, porque se o braço tende a se deslocar para a esquerda isso implica que a roda vai ter que girar no sentido anti-horário.
Sabendo então, a velocidade angular da roda, a velocidade em vai ser dada pela seguinte expressão:
Onde é dado por...
Desse modo;
Passo 3
Com isso, olhando a figura podemos obter a velocidade em , que será dada por...
E a velocidade de em relação à vai valer zero...
Consequentemente a velocidade angular da barra vai valer...
Passo 4
b) Continuando nosso raciocínio. Vamos fazer o esboço agora do que acontece quando vale .
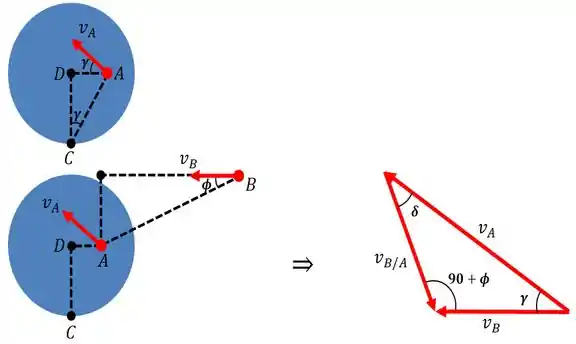
Bem! Já sabemos que...
Com base nisso, podemos determinar a velocidade em , que segundo a figura vai valer...
Passo 5
Falta obter !
É pra já! Pela figura esboçada, temos que...
E com isso, podemos obter com base na seguinte relação...
Desse modo...
Agora, vamos tratar de obter e !
Ora bolas! É só dar uma olhada no triângulo de velocidades que esboçamos e usar a lei dos senos...
O ângulo , nós podemos obter como sendo igual à...
E consequentemente, o ângulo vai valer...
Assim, podemos obter o que queremos...
será igual à...
E vai valer...
Obtido , somos capazes de achar a velocidade angular da barra ...
Pronto! Terminamos aqui! Até a próxima, guys!
Resposta
a)
b)