Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 25
5.25. Use the results of Sample Problem 5/3 to compute the coordinates of the mass center of the portion of the solid homogeneous cylinder shown.
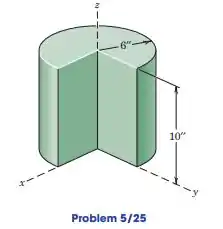
Passo 1
O problema fala de um resultado que a gente obteve lá no problema exemplo 5/3 do livro. Vamos lembrar que problema é esse:
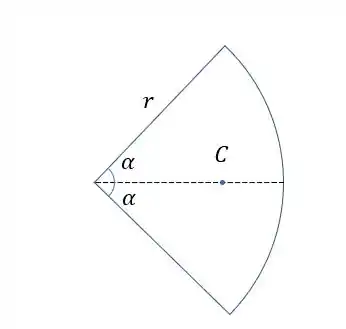
E daqui a gente tirou que o centro de massa é:
Esse resultado vai ser bem útil para gente, porque esse problema também trata de uma fração de um círculo. As faces do sólido que estão no plano são a fração de circulo que vamos nos concentrar inicialmente.
Passo 2
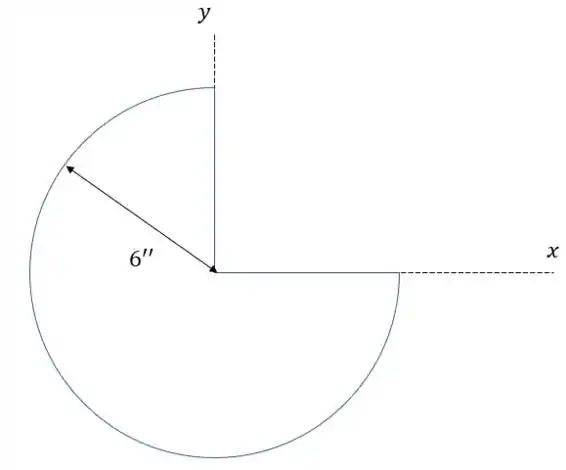
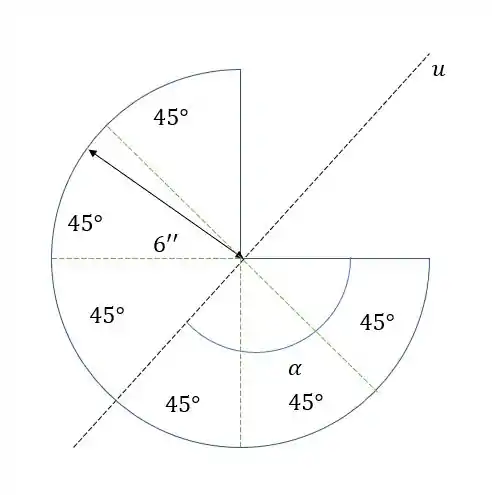
Essa é uma visão de cima do nosso sólido. Para ficar mais parecido com o exemplo que vamos usar para ajudar a gente, podemos criar um novo eixo, que corte nossa figura em duas partes iguais.
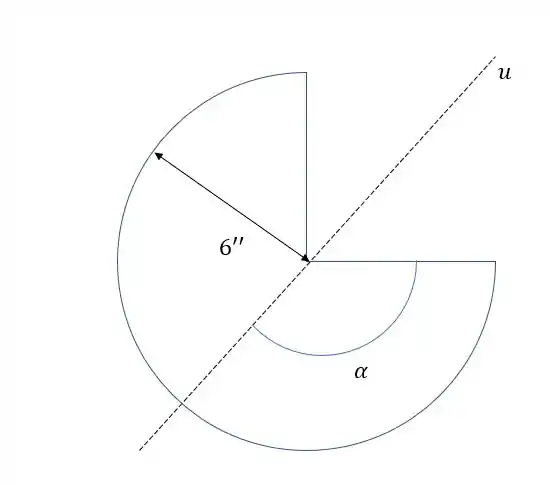
Então podemos escrever que
Primeiro vamos ver quem é esse . Se a gente dividir essa fração de círculo em partes iguais de , podemos ver facilmente que .
Ou então
E o raio é dado na imagem,
Então a nossa equação fica
Fazendo essas continhas
Passo 3
Achamos o ponto do centro de massa no eixo , agora vamos transpor para os eixos e . Para fazer isso é muito simples, repare que se transformamos tudo em vetor, vamos ficar com algo mais ou menos assim:
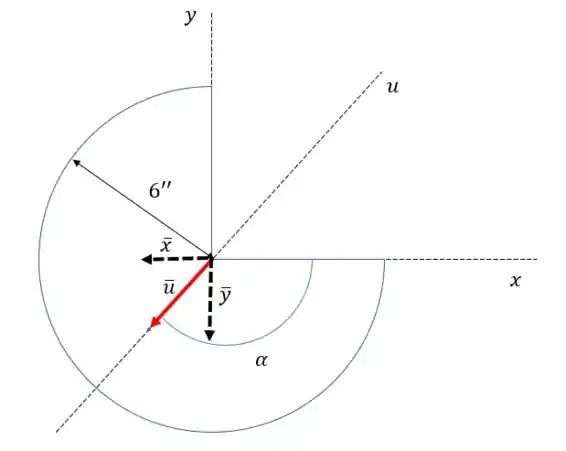
Podemos dizer que
Por simetria:
Então
Passo 4
Agora a gente só precisa achar o centro de massa no eixo . E isso não vai ser nada complicado, porque o sólido tem massa homogênea e além disso é perfeitamente simétrico no eixo , isso significa que o centro de massa está exatamente no meio
Então