Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 6

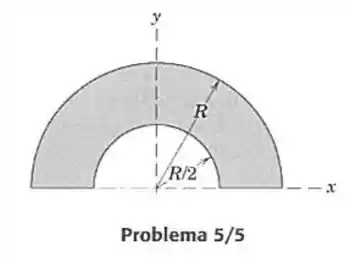
5- Determine, por integração direta, a coordenada y do centroide da área sombreada.

Passo 1

Desenhando nosso y médio na figura nós teremos:

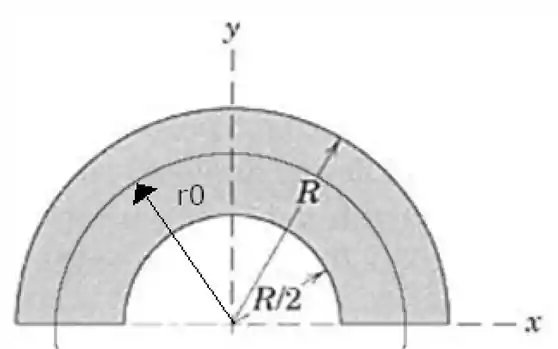
E para corpos circulares a análise em coordenadas polares é muito mais fácil e no exemplo 1 temos que nossa coordenada média em y será de:

y c = r 0   s e n   α α

Onda r 0 é a distância do centro até o raio médio e α será a metade do ângulo total percorrido, que no caso da figura será de:

α = π 2

Logo:

y c = r o   s e n π 2 π 2 = 2 r 0 π

Passo 2

No exemplo 3 encontra-se a área como:

d A = 2 r 0 α d r 0

Porque a área pode ser dada como:

A = r 2 2 α 2

Mas como α = π 2 teremos:

d A = π r 0   d r 0

Calculando a área nós teremos a seguinte integral, uma vez que r 0 varia de r 2 até r :

A = ∫ r / 2 r π r 0   d r 0 = π r 0 2 2 r / 2 r = π 2 r 2 - r 2 4 = 3 r 2 4 × π 2 = 3 π r 2 8

Passo 3

Para calcular y - temos que fazer.

y - = ∫ y c   d A A

Onde:

∫ y c d A = ∫ 2 r 0 π   π r 0   d r 0

Onde:

∫ r / 2 r 2   r 0 2 = 2 r 0 3 3 r / 2 r = 2 r 3 3 - 2 r 3 3 × 8 = 16 r 3 - 2 r 3 24 = 7 r 3 12

Agora dividindo esse resultado pela área temos:

y - = 7 r 3 12 3 π r 2 8 = 14 r 9 π

Resposta

y - = 14 r 9 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

22- Determine a coordenada y do centroide da área sombreada.
24- Determine as coordenadas do centroide da área sombreada
25- Determine as coordenadas x e y do centroide da área sombreada.
2- Faça com seu lápis um ponto sobre a posição da sua melhor estimativa visual do centroide da área do setor circular. Verifique sua estimativa usando os resultados do Exercício 5/3.
Localize o centroide da área sombreada entre as duas curvas.