Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 30
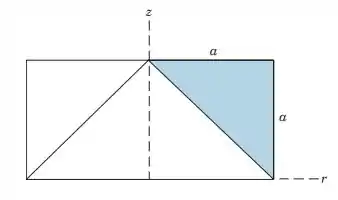
5.30. Determine the z-coordinate of the centroid of the volume generated by revolving the shaded area around the z-axis through 360°.
Passo 1
Vamos lá, queremos descobrir o centro de massa no eixo , e para isso vamos usar a equação
Primeiro vamos descobrir o elemento de área .
Essa é a vista de frente do sólido, mas ele vai ser revolucionado, então se olharmos de cima só para essa marca vermelha que fizemos vamos ter algo assim:
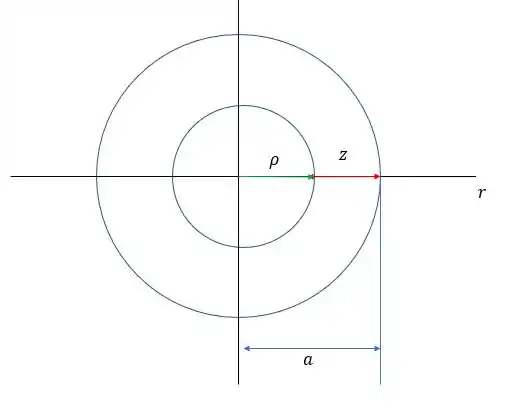
A gente pode dizer que essa largura é sempre igual a , se você olhar bem a figura vai perceber que o triângulo que usamos de referencia está dentre de um quadrado, isso nos dá uma simetria interessante que entrega esse resultado para a gente.
Então o elemento de volume é
E a área é a área entre os dois círculos da imagem. Vamos definir , e temos
Então
Logo
Passo 2
Vamos continuar encontrando o volume da figura
Isso fica
Então o volume é:
Passo 3
Agora finalmente podemos encontrar o ponto .
Isso fica
Resolvendo essa integral
Então
E chegamos a um resultado!