Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 34

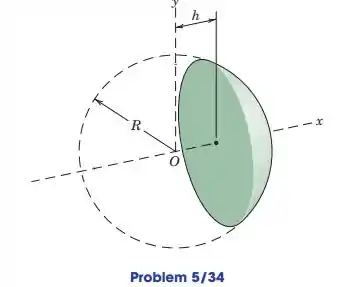
5.34. Determine the x-coordinate of the centroid of the solid spherical segment. Evaluate your expression for h = R 4 and h = 0 .

Passo 1

Vamos lá, queremos descobrir o centro de massa no eixo y , e para isso vamos usar a equação

x - = ∫ x c d V V

Primeiro vamos descobrir o elemento de área d V .

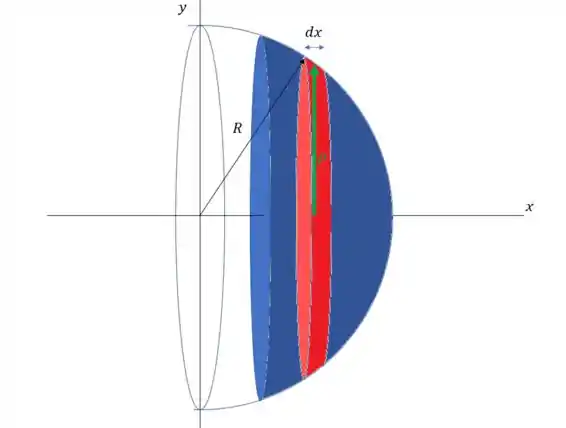
Então o elemento de volumo vai ser o volume desse pequenho cilindro de comprimento d x e raio ρ . Mas olha só, esse raio ρ vai mudar com x , podemos usar uma relação para determinar esse raio

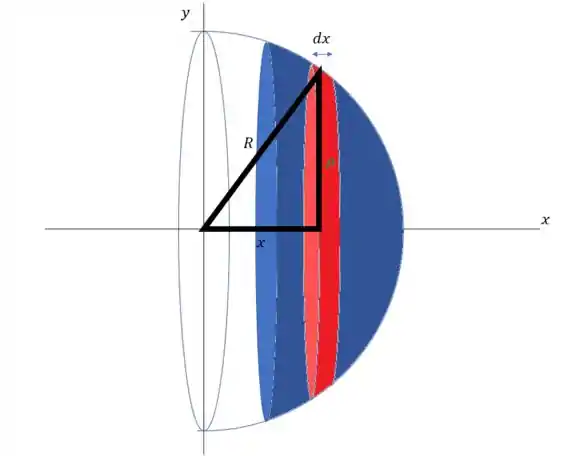
Por esse triângulo podemos ver que

R 2 = x 2 + ρ 2

Então

ρ 2 = R 2 - x 2

Agora vamos determinar o volume do cilindro:

d V = π ρ 2   d x

Então

d V = π R 2 - x 2   d x

Passo 2

Beleza, agora vamos determinar o volume do nosso sólido, para isso é só usar a integral

V = ∫ d V

Então

V = π R 2 - x 2   d x

Os limites a gente vê na imagem, o sólido começa em x = h e termina em x = R , então

V = ∫ h R π R 2 - x 2   d x

Isso fica

V = π R 2 x - x 3 3 h R

Logo

V = π R 3 - R 3 3 - R 2 h - h 3 3

Então o volume é

V = 2 3 R 3 π - π h R 2 - h 2 3

Passo 3

Agora vamos finalmente usar a integral para descobrir a coordenada de z do centro de massa.

x - = ∫ h R x V d V

Substituindo V e d V

x - = ∫ h R x 2 3 R 3 π - π h R 2 - h 2 3 d V

Isso aqui fica

π R 2 - x 2   d x

x - = 1 2 3 R 3 π - π h R 2 - h 2 3 ∫ h R π R 2 x - π x 3   d x

Então

x - = 1 2 3 R 3 π - π h R 2 - h 2 3 π R 2 x 2 2 - π x 4 4 h R

Substituindo esses valores

x - = 1 2 3 R 3 π - π h R 2 - h 2 3 π R 4 2 - R 2 h 2 2 - R 4 4 - h 4 4

E a gente pode simplificar para

x - = 1 2 3 R 3 π - π h R 2 - h 2 3 π R 4 4 - h 2 2 R 2 - h 2 2

Passo 4

Agora vamos substituir os valores que o enunciado pede, primeiro h = R 4

Vamos substituir isso na equação

x - = 1 2 3 R 3 π - π R 4 R 2 - R 2 48 π R 4 4 - R 2 32 R 2 - R 2 32

E isso aqui tudo vira

x - = R 4 4 - R 2 32 R 2 - R 2 32 2 3 R 3 - R 3 4 1 - 1 48

Isso fica

x - = R 4 R 3 1 4 - 1 32 1 - 1 32 2 3 - 1 4 1 - 1 48

x - = R 225 1024 27 64 = 25 48 R

Agora vamos fazer para h = 0

x - = 1 2 3 R 3 - 0 R 2 - 0 2 3 R 4 4 - 0 2 2 R 2 - 0 2 2

Então

x - = 1 4 R 4 2 3 R 3 = 3 8 R

Resposta

x - = 25 48 R

x - = 3 8 R

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.57. Determine the distance from the bottom of the base plate to the centroid of the built-up structural section shown.
5.32. Locate the centroid of the shaded area between the ellipse and the circle.
5.55. Determine the x- and y-coordinates of the centroid of the shaded area.
5.61. Determine the coordinates of the center of mass of the bracket, which is made from a plate of uniform thickness.
5.56. Determine the y-coordinate of the centroid of the shaded area.