Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 26

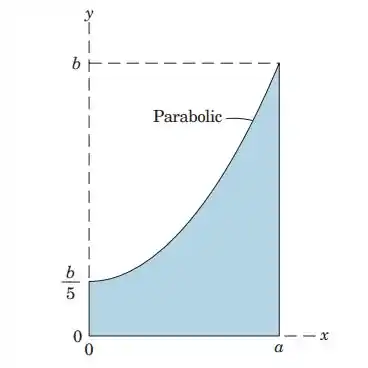
5.26. Determine the y-coordinate of the centroid of the shaded area shown.

Passo 1

Vamos lá, temos uma parábola e queremos descobrir o centro de massa no eixo y , e para isso vamos usar a equação

y - = ∫ y c d A A

Primeiro vamos descobrir o elemento de área d A .

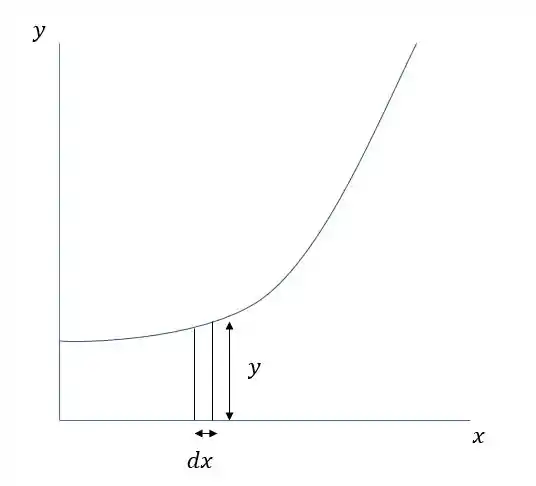
Então

d A = y   d x

E como temos um retângulo aqui podemos dizer que

y c = y 2

Passo 2

Agora pra prosseguir com a questão nós temos que deduzir a equação dessa parábola. Olha só, a parábola é uma função do tipo

y = A + B x 2

Para descobrir A , basta fazermos x = 0 , na figura vai ser quando a parábola está no eixo y , então

A = b 5

Agora para descobrir B vamos usar um ponto da função, podemos usar y = b , e x = a , que é um ponto que conhecemos

b = b 5 + B a 2

Então

B = 4 5 b a 2  

Então nossa equação fica

y = A + B x 2

y = b 5 + 4 5 b a 2   x 2

Passo 3

Agora vai ser simples calcular a área da parábola, basta fazer

A = ∫ 0 a b 5 + 4 5 b a 2   x 2 d x

Isso aqui fica

A = b 5 x 0 a + 4 15 b a 2 x 3 0 a

Então

A = a b 5 + 4 15 a b

Ou seja

A = a b 1 5 + 4 15 = 7 15 a b

Passo 4

Finalmente temos

y - = ∫ 0 a y 2   y   d x 7 15 a b

Isso fica

y - = 15 14 a b ∫ 0 a y 2   d x

y - = 15 14 a b ∫ 0 a b 5 + 4 5 b a 2   x 2 2   d x

Então temos

y - = 15 14 a b ∫ 0 a b 2 25 + 16 25 b 2 a 4 x 4 + 8 25 b 2 a 2   x 2   d x

Isso fica

y - = 15 14 a b b 2 25 x 0 a + 16 125 b 2 a 4 x 5 0 a + 8 75 b 2 a 2 x 3 0 a

Logo

y - = 15 14 a b b 2 a 25 + 16 125 b 2 a + 8 75 b 2 a

Podemos colocar b 2 a em evidencia

y - = 15 14 a b b 2 a 1 25 + 16 125 + 8 75

Isso aqui fica

y - = 15 14 b 103 375

E finalmente chegamos em

y - = 103 350 b

Resposta

y - = 103 350 b  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.55. Determine the x- and y-coordinates of the centroid of the shaded area.
5.63. Determine the coordinates of the mass center of the body constructed of a uniform square plate, a uniform straight rod, a uniform quarter-circular rod, and a particle (negligible dimensions). Th
Determine a coordenada y do centroide do volume gerado pela revolução da área sombreada do triangulo direito em torno do eixo z por 90 ° como mostrado na figura.
Determine a coordenada y do centroide do volume gerado pela revolução da área sombreada do triangulo direito em torno do eixo z por 90 ° como mostrado na figura.
Determine a coordenada y do centroide do volume gerado pela revolução da área sombreada do triangulo direito em torno do eixo z por 90 ° como mostrado na figura.