Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 63

5.63. Determine the coordinates of the mass center of the body constructed of a uniform square plate, a uniform straight rod, a uniform quarter-circular rod, and a particle (negligible dimensions). The mass of each component is given in the figure.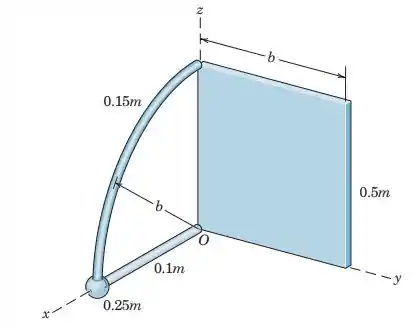

Passo 1

Beleza, vamos fragmentar o problema

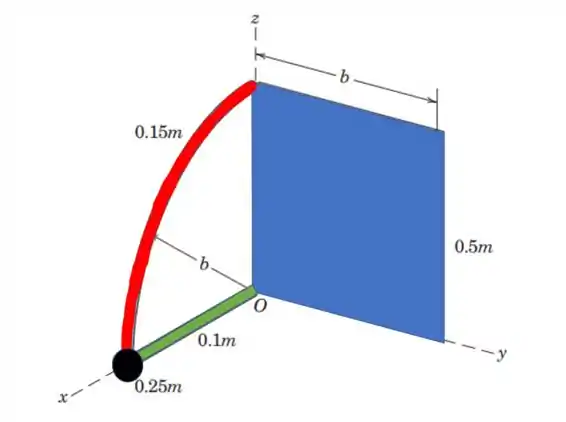
Então temos 4 figuras, uma de cada cor, nesse problema vamos começar a trabalhar com as massas da figura.

Passo 2

Podemos começar com o retângulo azul. Essa figura está contida no plano z y , então

x - 1 = 0

Agora vamos fazer para os eixos y e z .

y - 1 = b 2

E

z - 1 = b 2

Passo 3

Agora vamos para a figura em vermelho. Aquela figura é a borda de um quarto de círculo, que está contida no plano x z , para calcular o centroide dessa figura vamos precisar usar uma integral:

x - 2 = z - 2 = ∫ 0 π 2 r 2 sin ⁡ θ r π 2

Vamos resolver essa integral:

x - 2 = z - 2 = r 2 r π 2 - cos ⁡ θ ​ 0 π 2

Isso fica

x - 2 = z - 2 = r 2 r π 2 0 - - 1 = 2 r π

Como está na figura, r = b , então

x - 2 = z - 2 = 2 b π

E por estar em x z

y - 2 = 0

Passo 4

Agora vamos para a figura em verde, que é uma barra ao longo do eixo x , e por estar somente no eixo x podemos dizer que:

y - 3 = z - 3 = 0

Agora vamos calcular o centroide para essa barra:

x - 3 = b 2

Passo 5

Só falta a esfera preta. O raio dessa esfera é desprezível em relação ao resto da figura, então podemos considerar o centroide desse objeto como o ponto em que a esfera se encontra, então:

x - 4 = b y - 4 = 0 z - 4 = 0

Passo 6

Agora para calcular o centroide vamos usar a equação:

x - = ∑ m x - ∑ m

Isso fica

x - = m 1 x - 1 + m 2 x - 2 + m 3 x - 3 + m 4 x - 4 m 1 + m 2 + m 3 + m 4

Substituindo os valores

x - = 0,5 m ⋅ 0 + 0,15 m ⋅ 2 b π + 0,1 m ⋅ b 2 + 0,25 m ⋅ b 0,5 m + 0,15 m + 0,1 m + 0,25 m

Então

x - = 0,15 m ⋅ 2 b π + 0,1 m ⋅ b 2 + 0,25 m ⋅ b m

Podemos cortar m

x - = 0,15 ⋅ 2 b π + 0,1 ⋅ b 2 + 0,25 ⋅ b = 0,395   b

Agora vamos fazer para y - :

y - = ∑ m y - ∑ m

Isso fica

y - = m 1 y - 1 + m 2 y - 2 + m 3 y - 3 + m 4 y - 4 m 1 + m 2 + m 3 + m 4

Substituindo os valores

y - = 0,5 m ⋅ b 2 + 0,15 m ⋅ 0 + 0,1 m ⋅ 0 + 0,25 m ⋅ 0 0,5 m + 0,15 m + 0,1 m + 0,25 m

Então

y - = 0,5 m ⋅ b 2 m = 0,25 b

E finalmente

z - = ∑ m z - ∑ m

Isso fica

z - = m 1 z - 1 + m 2 z - 2 + m 3 z - 3 + m 4 z - 4 m 1 + m 2 + m 3 + m 4

Substituindo os valores

z - = 0,5 m ⋅ b 2 + 0,15 m ⋅ 2 b π + 0,1 m ⋅ 0 + 0,25 m ⋅ 0 0,5 m + 0,15 m + 0,1 m + 0,25 m

Então

z - = 0,5 m ⋅ b 2 + 0,15 m ⋅ 2 b π m = 0 , 3455 b

Resposta

x - = 0,395 b y - = 0,25 b z - = 0,3455 b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.34. Determine the x-coordinate of the centroid of the solid spherical segment. Evaluate your expression for h = R 4 and h = 0 .
5.26. Determine the y-coordinate of the centroid of the shaded area shown.
5.30. Determine the z-coordinate of the centroid of the volume generated by revolving the shaded area around the z-axis through 360°.
5.31. The figure represents a flat piece of sheet metal symmetrical about axis A-A and having a parabolic upper boundary. Choose your own coordinates and calculate the distance from the base to the ce
5.25. Use the results of Sample Problem 5/3 to compute the coordinates of the mass center of the portion of the solid homogeneous cylinder shown.