Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 55
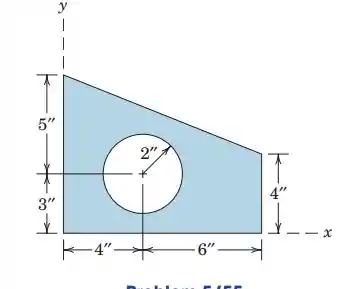
5.55. Determine the x- and y-coordinates of the centroid of the shaded area.
Passo 1
Vamos em busca de mais um centroide!
Como sempre, vamos separar a figura em várias figuras mais fáceis de resolver:
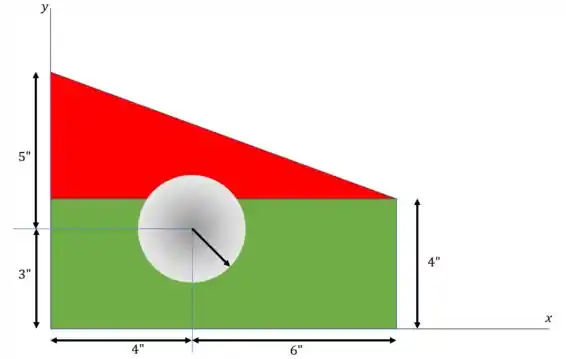
Então temos três figuras: O retângulo verde, o triângulo vermelho e o círculo branco. Atenção, esse círculo aí é uma parte que falta na figura, então a gente vai considerar valores negativos para ele.
Passo 2
Vamos começar pelo retângulo. A área de um retângulo é sempre o produto de sua base pela altura, então:
Agora vamos calcular o centroide. As coordenadas do centroide do retângulo são bem simples:
E
Passo 3
Agora vamos para o triângulo em vermelho. Vamos começar com a área, pode ser um pouco difícil encontrar a altura desse triângulo, mas basta subtrair a altura do retângulo da altura total da figura:
Então
Exatamente a metade da área do retângulo, e isso é lógico, porque esse triângulo é como se fosse aquele retângulo cortado no meio.
Beleza, agora vamos para o centroide, mas aqui a gente vai ter que mudar o centro do eixo de coordenadas.
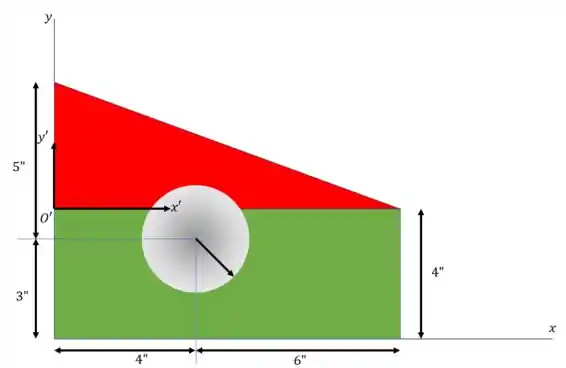
Agora o centro do eixo de coordenadas está em , no ponto do sistema original de coordenadas.
Vamos lá
E
Agora vamos passar isso para o sistema original de coordenadas, usando a equação
Então
E
Então
Passo 4
Agora vamos para o círculo. A área do círculo é
Agora vamos calcular o centroide, e não vai ser nada complicado, porque para nossa sorte o círculo é uma figura totalmente simétrica, então seu centroide é exatamente no seu centro, e o centro do círculo está marcado na figura.
E
Mas lembre-se que o peso das componentes do círculo para o centroide da figura toda vai ser negativo.
Passo 5
Agora podemos finalmente calcular o centroide da figura toda, vamos começar com o eixo
Isso fica
Substituindo os valores
E agora vamos fazer o mesmo para
Isso fica
Substituindo os valores
E terminamos mais uma questão.